6. Základy kinetické teorie
Obsah
Sylabus
Základy kinetické teorie Maxwellovo-Boltzmannovo rozdělení, tlak, teplota, vnitřní energie. Transportní jevy v plynech. Molekulární jevy v kapalinách, Avogadrovo číslo.
Maxwellovo-Boltzmannovo rozdělení, tlak, teplota, vnitřní energie
Molekulová fyzika vykládá chování makroskopických systémů z vlastností molekul a ze statistických zákonitostí, ale vzájemné chování molekul popisuje fenomenologicky, aniž by se snažila o jeho vysvětlení. Důležitou charakteristikou pohybu molekul je jejich rychlost.
Maxwellovo-Boltzmannovo rozdělení
Vyjdeme z předpokladu, že hustota pravděpodobnosti nalezení částice v elementárním objemu fázového prostoru je
$ dP(q,p)=N \exp{\left(-\frac {E} {k_B T}\right) } dp dq $
kde $ N $ je normovací konstanta, $ k_B $ Boltzmanova konstanta, $ T $ absolutní teplota a $ E $ energie. Pokud lze energii napsat jako součet kinetické a potenciální $ E=T(p)+V(q) $ (pozor, tady je $ T $ kinetická energie a ne teplota), můžeme výpočet rozdělit na 2 části, Maxwellovo rozdělení pro kinetickou energii a Boltzmannovo pro potenciální.
Pro ideální plyn je $ V $ konstantní, za energii dosadíme kinetickou $ T= \frac {p^2} {2 m} $ a úpravou výrazu (spočtení normovací konstanty, substituce hybnosti za rychlost, převedení do sférických souřadnic a částečná integrace (přes úhlové proměnné))
$ dP(p)= C \exp{\left( - \frac {p_x ^2+p_y ^2+p_z ^2} {2 m k_B T}\right)} dp_x dp_y dp_z $
získáváme výraz pro M.B. rozdělení velikosti rychlosti molekul ideálního plynu
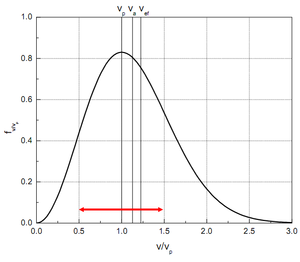
$ dP(v)=4 \pi \left( \frac {m} {2 \pi k_B T} \right)^{3/2} v^2 \exp{\left(- \frac {m v^2} {2 k_B T}\right)} dv $
Tvar rozdělení lze experimentálně ověřit přímým měřením. Máme 2 rotující souosé kotouče, první má štěrbinu, pouštíme na ně molekuly z pícky. Molekuly, které prolétly štěrbinou, se zachytí na druhém kotouči v poloze, která odpovídá rovnici
$ v=\frac {d} {\phi} \omega $
kde $ d $ je vzdálenost kotoučů, $ \omega $ úhlová rychlost jejich otáčení a $ \phi $ úhel, o který se desky pootočí během průlety molekuly mezi nimi.
Počet molekul dané rychlosti je pak úměrný tloušťce vrstvy na příslušném místě druhého kotouče.
Zintegrováním lze spočíst střední rychlost
$ \overline v = \sqrt { \frac {8 k_B T} {\pi m}} $
nejpravděpodobnější rychlost - kterou má nejvíce molekul - (derivace rozdělení se položí rovna nule)
$ v_p = \sqrt { \frac {2 k_B T} {m}} $
střední kvadratickou rychlost (plyne i z ekvipartičního teorému), tzv. efektivní rychlost:
$ \overline {v^2} = \left( \sqrt { \frac {3 k_B T} {\ m}} \right)^2 $
Pro představu střední aritmetická $ v_{a} = 1,128 \cdot v_p $ a $ v_{ef} = 1,225 \cdot v_p $
Tlak
Tlak je definován vztahem $ p= \frac {F} {S} $. V rámci kinetické teorie plynů můžeme tlak vysvětlit nárazy molekul na stěnu nádoby. Pohyb molekul je zcela chaotický, pohybují se libovolnými směry se všemi velikostmi rychlostí. Při dokonale pružném nárazu molekuly na stěnu se změní její hybnost o $ \delta p = 2 m v \ $.
Pro velikost tlaku plynu lze odvodit vztah
$ p= \frac {1}{3} \frac {N m} {V} \overline {v^2} = \frac {1}{3} \rho \overline {v^2} $
Odvození
Na plošku stěny systému $ \Delta S $ ze všech směrů padají částice a předávájí hybnost, když vezmeme koncetraci částic $ n = \frac{N}{V} $ je výsledný integrál tento:
$ p = \frac{1}{\Delta S} 2 \int_{0}^{\pi / 2} \int_{0}^{2\pi} \int_{0}^{\infty} n f_v m v^2 \Delta S \cos^2 \theta \sin \theta v^2 \mathrm{d}v \mathrm{d}\Phi \mathrm{d}\theta = \frac{nm}{3} \int_0^{\infty}v^2 f_v 4\pi v^2 \mathrm{d}v $
$ p = \frac{1}{3} n m \overline {v^2} $
Teplota
Pro ideální plyn platí předchozí vzorec $ p V= \frac {1}{3} N m \overline {v^2} $
a zároveň stavová rovnice $ p V= n R T \ $, kde $ R=8,3143 \, \rm J\, K^{-1}\, mol^{-1} \ $ je plynová konstanta a $ n $ látkové množství.
Porovnáním obou vztahů získáme vztah pro teplotu:
$ T= \frac {M_m} {3 R} \overline {v^2} $
kde $ M_m $ je molární hmotnost daného plynu.
Podle kinetické teorie je teplota veličina, která charakterizuje intenzitu chaotického pohybu souboru molekul.
Vnitřní energie
Celkovou kinetickou energii translačního pohybu $ N $ molekul můžeme napsat jako
$ E=\sum_{i=1}^N \frac {1}{2} m v_i ^2 = \frac {1}{2} N m \overline {v^2} $
Porovnáním s rovnicí pro tlak získáme
$ E= \frac {3 n R T}{2} $
U jednoatomového plynu se uplatňuje pouze translační pohyb, vnitřní energie je tedy rovna kinetické $ U= \frac {3 n R T}{2} $
Pro dvouatomové molekuly musíme započíst i rotaci a dostaneme vztah $ U= \frac {5 n R T}{2} $
Ekvipartiční teorém říká, že na každý stupeň volnosti molekuly přísluší střední hodnota kinetické energie $ \frac {k_B T} {2} $
$ nR=Nk_B \ $
Transportní jevy v plynech
Termodynamická soustava se může vnějším zásahem dostat do nerovnovážného stavu, např. stlačování plynu, zahřívání stěny nádoby,... Soustava se pak snaží dostat zpět do rovnovážného stavu s maximální entropií. Transportní jevy jsou nerovnovážné děje, při nichž dochází k vyrovnání určité fyzikální veličiny. Patří mezi ně viskozita, kdy dochází k přenosu hybnosti, vedení tepla, přenos energie, a difuze, transport hmoty.
Všechny tyto jevy lze popsat obecným vzorcem
$ i=-\alpha \frac{dA}{dx} $
kde $ i $ je tok - množství veličiny přenesené za jednotku času jednotlivou plochou, popisuje rychlost transportního děje, $ \alpha $ je součinitel transportního jevu a $ \frac{dA}{dx} $ je gradient příslušné veličiny. Záporné znaménko vyjadřuje, že přenos probíhá ve směru poklesu dané veličiny.
Transportní jev probíhá tím rychleji, čím je intenzivnější tepelný pohyb molekul. Ty se při svém pohybu vzájemně srážejí a lze odvodit výraz pro střední volnou dráhu $ \overline l $ - průměrná délka trajektorie, na níž nedojde ke srážce.
$ \overline l = \frac {1}{\sigma n_V} $
kde $ n_V =\frac {N}{V} $ je hustota molekul a $ \sigma = 4 \pi r^2 \ $ účinný srážkový průřez, který je úměrný ploše zabírané molekulou o poloměru $ r $.
Odvození vztahu pro střední volnou dráhu se dá přibližně, zato však jednoduše provést představou, že všechny částice kromě jedné zmrazím. Ta volná se pohybuje a vytyčuje v prostoru sloupeček o poloměru r a délce vdt. Když n je koncentrace částic tak odvození je
$ \overline l = \frac{v \cdot \mathrm{d}t}{v\mathrm{d}t \cdot \pi (2r)^2 n}= \frac{1}{\pi (2r)^2 n} $
To má pouze tu vadu na kráse, že ostatní částice se také hýbou, takže střední dráha je pak menší a to $ \frac{1}{\sqrt{2}} $-krát.
Viskozita - Vnitřní tření
Protéká-li plyn trubicí, vykonávají molekuly plynu kromě tepelného pohybu ještě uspořádaný pohyb. Velikost rychlosti tohoto uspořádaného pohybu není ve všech vrstvách plynu konstantní, ale je funkcí vzdálenosti od stěny trubice. Mezní vrstva, která je v kontaktu se stěnou, je v klidu.
Molekuly, které se přesunou z rychlejší vrstvy do pomalejší, mají větší hybnost než odpovídá průměrné hybnosti v pomalejší vrstvě. Při přesunu do rychlejší naopak mají hybnost menší než průměrná, docházelo by tedy k vyrovnání rychlostního gradientu. Pokud má být tok ustálený, musí působit vnější síla, která je realizovaná rozdílem tlaků na koncích trubice.
Hustota toku hybnosti je úměrná síle působící mezi vrstvami (ta je daná přenesenou hybností).
Newtonův zákon viskozního toku má tvar
$ i=\frac {F}{S}=- \eta \frac {\partial v}{\partial x} $
a zavádí dynamickou viskozitu $ \eta $. Odvozením výrazu pro hustotu toku a dosazením za $ \overline l $ a $ \overline v $ (z M.-B. rozdělení) získáme:
$ \eta =\frac {1}{2} \rho \overline l \overline v = \frac {1}{4 \pi r^2} \sqrt {\frac {m_0 k_B T}{\pi} } $
kde $ \rho =m_0 n_V \ $ je hustota plynu.
Dynamická viskozita nezávisí na na tlaku a hustotě plynu. Její jednotkou je Pa.s
Vedení tepla
Mějme vodorovnou trubici s konci udržovanými na různých teplotách. Molekuly v oblasti s vyšší teplotou mají větší kinetickou energii. Volným pohybem se dostávají do chladnější oblasti a díky srážkám předávají část své energie chladnějším molekulám. Obdobně pro pomalejší molekuly. Takto dochází k přenosu energie z teplejší oblasti do chladnější. Kdybychom neudržovali konstantní teploty na koncích trubice, došlo by k vyrovnání teploty.
Vedení tepla můžeme popsat pomocí gradientu teploty, protože teplota je u ideálních plynů úměrná vnitřní energii.
$ q= - \lambda \frac {dT} {dx} $
kde $ q $ je hustota tepelného toku a $ \lambda $ součinitel tepelné vodivosti, který určíme z úvah o střední energii molekul pomocí měrné tepelné kapacity $ c_v $
$ \lambda = \frac {1} {2} \rho \overline v \overline l c_v = \eta c_v $
$ \lambda $ je nezávislé na tlaku, pouze u velmi nízkých tlaků s tlakem klesá, což je způsobeno tím, že $ \overline l $ je větší než vzdálenost desek, mezi kterými se plyn pohybuje. Toho se využívá v Dewarových nádobách, kde mezi zdvojenými stěnami je silně zředěný vzduch, který se chová jako dobrý tepelný izolátor.
Rovnice vedení tepla, tak jak ji známe z matematiky, vypadá takto:
$ \frac{\partial T}{\partial t}= \frac{\lambda}{\rho c_v} \frac{\partial^2 T}{\partial x^2} $
Fundamentální řešení má tvar
$ f(x,t)= \frac {1} {\sqrt {4 \pi \alpha t} } \exp\left(- \frac {x^2} {4 \alpha t}\right) $
a obecné řešení získáme konvolucí s počáteční podmínkou.
Difuze
Středoškolská definice říká: difuze je samovolné pronikání částic jedné látky mezi částice látky druhé, jsou-li tělesa z těchto látek uvedena do vzájemného styku. Odborněji to je pohyb částic vyvolaný gradientem, např. teplotním nebo koncentračním.
Příčinou difuze je rozdíl v hustotě molekul v různých místech prostoru, nehraje tam roli tlak.
Rovnice difuze vypadá takto:
$ i=- D \nabla n $
případně po dosazení zákona zachování počtu částic $ \frac {\partial n}{\partial t} + \nabla \cdot \mathbf{i} = 0 $
$ \frac{\partial n}{\partial t}= D \Delta n $
$ D=\frac{1}{6} \overline l \overline v $ je koeficient difuze
kde $ i $ je hustota difuzního toku, $ n $ hustota molekul, $ \overline l $ střední volná dráha a $ \overline v $ střední rychlost ve směru difuze. Vztah platí jen přibližně a lze ho odvodit z úvah o počtu částic, které projdou přes přepážku, která původně plyny oddělovala.
Teplotní závislost koeficientu difuze $ D $ je dána teplotní závislostí $ \overline v $ a určuje tzv. termofúzi. Je-li ve směsi plynů gradient teploty, molekuly lehčího plynu se pohybují ve směru vzrůstu teploty, těžší naopak. Toho lze použít k oddělování molekul.
Molekulární jevy v kapalinách, Avogadrovo číslo
Látky kapalného skupenství tvoří přechod mezi látkami pevnými a plynnými. Skládají se z molekul, které jsou v neustálém neuspořádaném pohybu, o němž svědčí např. difuze nebo Brownův pohyb. Tepelný pohyb molekul kapalin je podobný pohybu molekul plynů, ale nemá tak velkou kinetickou energii. Na rozdíl od plynů ale mají molekuly krátkodosahové uspořádání - molekuly jsou vázány do skupin, které jsou uspořádané, ale pohybují se neuspořádaným pohybem vůči ostatním skupinám molekul.
K molekulárním jevům v kapalinách řadíme transportní jevy, vlastnosti povrchové vrstvy a kapilární jevy v úzkých trubicích.
Dále se ještě lze zmínit o jevech na rozhraní 3 prostředí a tlaku pod zakřiveným povrchem kapaliny.
Transportní jevy
Transportní jevy v kapalinách jsou obdobné transportní jevy v plynech.
Patří mezi ně:
Difuze, která však probíhá pomaleji než v plynech.
Vnitřní tření - dynamická viskozita je řádově větší než u plynů a s rostoucí teplotou se exponenciálně zmenšuje.
Vedení tepla - pokud kapalinu zahříváme ode dna, dochází k proudění, kdy se teplejší molekuly, které jsou lehčí, snaží dostat k hladině a naopak.
Povrchová vrstva
Molekuly kapaliny jsou u sebe mnohem blíže než molekuly plynu, působí na sebe přitažlivými silami a vyvolávají tak vnitřní tlak. Pokud je molekula hluboko pod povrchem, síly od ostatních molekul, které na ní působí, se vzájemně vyruší. Výslednice sil působících na molekuly u povrchu však míří dovnitř kapaliny, kolmo k volnému povrchu, a je největší pro molekuly přímo na povrchu. Povrchová vrstva tedy působí na ostatní kapalinu tlakovou silou a vyvolává uvnitř kapaliny kohezní (vnitřní) tlak, velikosti řádově GPa.
Jednou ze složek vnitřní energie kapaliny je povrchová energie, která je dána rozdílem potenciální energie molekul v povrchové vrstvě oproti energii, kterou by měly uvnitř kapaliny. Přírůstek povrchové energie $ \delta E_S $ lze vyjádřit pomocí kapilární konstanty $ \sigma* $, která má význam plošné hustoty energie, a přírůstku obsahu plochy kapaliny $ \delta S $.
$ \delta E_S= \sigma* \delta S \ $
Protože rovnovážný stav soustavy odpovídá minimu potenciální energie, snaží se kapalina zmenšit svůj povrch na minimum, což vede k tvorbě kapek nebo mýdlových blan s minimálním povrchem.
Na povrchu kapaliny působí na molekuly povrchová síla $ \mathbf{F} $ rovnoběžná s povrchem. Pomocí ní definujeme povrchové napětí $ \sigma $ jako
$ \sigma= \frac {dF} {dl} $
Pokusem s napnutou blánou na rámečku s pohyblivou příčkou, rovností vykonané práce na posunutí příčky a změny povrchové energie dojdeme ke vztahu $ \sigma= \sigma * \ $
Kapilární jevy
Ponoříme-li úzkou trubici malého vnitřního průměru svisle do kapaliny, pozorujeme zakřivení povrchu kapaliny v trubici a její vzestup nebo snížení vzhledem k hladině kapaliny v nádobě. Pokud kapaliny smáčí stěny trubice, nastává kapilární elevace, pokud nesmáčí, tak kapilární deprese.
Elevační výšku $ h $ určíme z úvah o vyrovnání působících tlaků: atmosférický, kohézní, hydrostatický, kapilární (vzniká zakřivením povrchu kapaliny)
$ h= \frac {2 \sigma} {r (\rho - \rho _0) g} $
kde $ r= \frac {R} {cos{\theta}} $ je poloměr křivosti hladiny, $ R $ poloměr kapiláry, $ \theta $ krajní úhel mezi kapalinou a kapilárou, $ g $ tíhové zrychlení, $ \rho $ hustota kapaliny a $ \rho_0 $ hustota okolního vzduchu.
Avogadrova konstanta
Je definována jako počet atomů v 12 g izotopu uhlíku 612C . Udává počet částic v 1 molu látky.
Její hodnota je
$ N_A =6,0221415.10^{23} \mbox{mol}^{-1} \, $
a lze určit při studiu Brownova pohybu, viz 4. Struktura látek.
$ N_A = \frac{RTt}{3\pi\eta r \overline{x^2}} $
kde $ R $ je molární plynová konstanta, $ T $ teplota, při které probíhá měřění, $ t $ doba měřění, $ \eta $ viskozita roztoku, v němž se částice pohybují, $ r $ poloměr studovaných částic a $ \overline{x^2} $ je průmět středního kvadratického posunutí částice pro 1D pohyb.
Zdroj: E. Svoboda, R. Bakule: Molekulová fyzika