Státnice - NP-úplnost
Obsah
|
Tohle je poněkud obšírnější výcuc ke státnicovým okruhům ze složitosti pro obory Matematická lingvistika a Softwarové systémy, pocházející ze zápisků z předmětu Složitost I -- Tuetschek 22:44, 16 Aug 2010 (CEST)
Třídy P a NP, polynomiální převody, NP-úplnost
Definice (Úloha)
- Úloha je situace, kdy pro daný vstup (instanci úlohy) chceme získat výstup se zadanými vlastnostmi.
- Optimalizační úloha je úloha, kde cílem je získat optimální (zpravidla největší nebo nejmenší) výstup s danými vlastnostmi.
- Rozhodovací problém je úloha, jejímž výstupem je ANO/NE.
Definice (Kódování vstupů)
Každá instance problému $ Q\,\! $ je kódována jako posloupnost 0 a 1, tj. instance je slovo v abecedě $ \{0,1\}^{*}\,\! $. Kódy všech instancí problému $ Q\,\! $ tvoří jazyk $ L(Q)\,\! $ nad abecedou $ \{0,1\}^{*}\,\! $, který se dělí na
- $ L(Q)_Y\,\! $ -- kódy instancí s odpovědí ANO (jazyk kladných instancí)
- $ L(Q)_N\,\! $ -- kódy instancí s odpovědí NE (jazyk záporných instancí)
Rozhodovací problém pak je rozhodnutí, zda $ x\in L(Q)_Y\,\! $ nebo $ x\in L(Q)_N\,\! $ (kde $ x\,\! $ je kód nějaké instance $ Q\,\! $), když předpokládáme, že rozhodnutí $ x\in L(Q)\,\! $ lze udělat v polynomiálním čase vzhledem k $ |x|\,\! $.
Definice (Deterministický Turingův stroj)
DTS obsahuje řídící jednotku, čtecí a zápisovou hlavu a (nekonečnou) pásku. Program sestává z:
- Konečné množiny $ \Gamma\,\! $ páskových symbolů, $ \Sigma \subset \Gamma\,\! $ vstupních symbolů a $ *\in\Gamma\,\! $ prázdného symbolu
- Konečné množiny $ Q\,\! $ stavů řídící jednotky, která obsahuje startovní stav $ q_0\,\! $ a 2 terminální stavy $ q_Y\,\! $, $ q_N\,\! $
- Přechodové funkce $ \delta:(Q\backslash\{q_Y,q_N\})\times\Gamma\to Q\times\Gamma\times\{\leftarrow,\bullet, \rightarrow \}\,\! $
DTS s programem $ M\,\! $ přijímá $ x\in\Sigma^{*}\,\! $, právě když pro vstup $ x\,\! $ se $ M\,\! $ zastaví ve stavu $ q_Y\,\! $. Jazyk rozpoznávaný programem M je $ L(M)=\{x\in\Sigma^{*}|M \mbox{ prijima } x\}\,\! $.
DTS s programem $ M\,\! $ řeší problém $ Q\,\! $, právě když výpočet $ M\,\! $ skončí pro každý vstup $ x\in\Sigma^{*}\,\! $ a platí $ L(M)=L(Q)_Y\,\! $.
Nechť $ M\,\! $ je program pro DTS, který skončí pro $ \forall x\in\Sigma^{*}\,\! $. Časová složitost programu $ M\,\! $ je dána funkcí $ T_M(n)=\max\{m|\exists x\in\Sigma^{*},|x|=n, $ výpočet na DTS s programem $ M\,\! $ a vstupem $ x\,\! $ skončí po $ m\,\; $ krocích stroje$ \}\,\! $. Pokud existuje polynom $ p\,\! $ tak, že $ T_M(n)\leq p(n) \forall n\,\! $, pak $ M\,\! $ je polynomiální DTS program.
Definice (Třída P)
Problém $ Q\,\! $ je ve třídě P, právě když existuje polynomiální DTS program $ M\,\! $, který řeší $ Q\,\! $.
Definice (Nedeterministický Turingův stroj)
Stejný jako DTS, ale místo přechodové funkce $ \delta\,\! $ je zde zobrazení $ \delta\,\! $, které každé dvojici z $ Q\times\Gamma\,\! $ přiřazuje množinu možných pokračování výpočtu, tj. trojic z $ Q\times\Gamma\times\{\leftarrow,\bullet, \rightarrow \}\,\! $.
NTS s programem $ M\,\! $ přijímá $ x\in\Sigma^{*}\,\! $, právě když existuje přijímající výpočet programu $ M\,\! $ (tj. běh $ M\,\! $, kdy na vstupu je $ x\,\! $ a končí se ve stavu $ q_Y\,\! $). Jazyk rozpoznávaný programem M je $ L(M)=\{x\in\Sigma^{*}|M \mbox{ prijima } x\}\,\! $.
Čas, ve kterém $ M\,\! $ přijímá $ x\in\Sigma^{*}\,\! $ definujeme jako počet kroků nejkratšího přijímajícího výpočtu nad daty $ x\,\! $.
Časová složitost programu je dána funkcí:
- $ T_M(n)=\begin{cases}1 \mbox{ neexistuje }x\mbox{ delky }n\mbox{, ktere je prijimano }\\\max\{m|\exists x\in\Sigma^{*},|x|=n, M\mbox{ prijima }x\mbox{ v case }m\}\end{cases}\,\! $
Pokud existuje polynom $ p\,\! $ takový, že $ T_M(n)\leq p(n)\,\! $, pak $ M\,\! $ je polynomiální NTS program.
Definice (Třída NP)
Problém $ Q\,\! $ je ve třídě NP, právě když existuje polynomiální NTS program $ M\,\! $, který řeší $ Q\,\! $. Na rozdíl od deterministického případu netrváme na tom, že výpočet musí skončit i pro nepřijímané instance.
Poznámka (Jiný model NTS)
Přidáme další pásku (orákulum) a stroj pracuje ve 2 fázích:
- Nedeterministicky hádá -- zapíše problém do orákula.
- Deterministicky ověřuje obsah orákula -- práce DTS na původním vstupu plus obsahu orákula.
Je to ekvivalentní s původním -- omezíme-li počet možných přechodů NTS na 2 (tím ho jen zpomalíme) a zapisujeme-li do orákula větve pokračování výpočtu (pak stačí na jednu jeden bit), převedeme veškerý nedeterminismus čistě na naplnění orákula.
Definice (Třída co-NP)
Problém $ Q\,\! $ je ve třídě co-NP, právě když existuje polynomiální NTS program $ M\,\! $ takový, že $ L(M) = L(Q)_N\,\! $. O poměru množin co-NP a NP nevíme nic, jen to, že podmnožinou jejich průniku je P.
Převody a NP-úplnost
Definice (Polynomiálně vyčíslitelná funkce)
Funkce $ f:\{0,1\}^{*}\to\{0,1\}^{*}\,\! $ je polynomiálně vyčíslitelná, právě když existuje polynom $ p\,\! $ a algoritmus $ A\,\! $ takový, že pro každý vstup $ x\in \{0,1\}^{*}\,\! $ dává výstup $ f(x)\,\! $ v čase nejvýše $ p(|x|)\,\! $.
Definice (Polynomiální převoditelnost)
Jazyk $ L_1\,\! $ je polynomiálně převoditelný na jazyk $ L_2\,\! $ (píšeme $ L_1\propto L_2\,\! $), právě když existuje polynomiálně vyčíslitelná funkce $ f\,\! $ taková, že
- $ \forall x\in\{0,1\}^{*}:x\in L_1\equiv f(x)\in L_2\,\! $
Definice (NP-těžký, NP-úplný problém)
- Problém $ Q\,\! $ je NP-těžký, právě když $ \forall Q'\in\mathrm{NP}:L(Q')_Y\propto L(Q)_Y\,\! $.
- Problém $ Q\,\! $ je NP-úplný, právě když je $ Q\,\! $ NP-těžký a $ Q\in\mathrm{NP}\,\! $.
Je-li nějaký NP-těžký problém převoditelný na jiný, pak ten musí být také NP-těžký.
Příklady NP-úplných problémů a převody mezi nimi
Upraveno podle vypracovaných otázek V. Bedecse, původně zřejmě ze slajdů Doc. Čepka k Složitosti I . -- Tuetschek 10:28, 31 Aug 2010 (CEST)
Cook-Levinova věta
Existuje NP-úplný problém.
Důkaz pro KACHL
Máme množinu barev $ B $, čtvercová síť $ S $ s obvodem obarveným barvami z $ B $ a množinu $ K $ typů kachlíků, kde je každý typ definován svou horní, dolní, levou a pravou barvou.
Lze síť $ S $ vykachlíkovat pomocí kachlíků z množiny $ K $ (stejný typ lze použít libovolněkrát, kachlíky ale nelze otáčet) tak, aby:
- barvy kachlíků přilehlé k obvodu sítě souhlasily s barvami předepsanými tomto na obvodu sítě a
- každá dvojice barev na dotyku dvou kachlíků byla rovněž shodná?
NP-úplné problémy
Splnitelnost (SAT)
CNF (booleovská formule v konjunktivní normální formě, tj. konjunkce disjunkcí) $ F $ na $ n $ proměnných. Existuje pravdivostní ohodnocení proměnných, které splňuje formuli $ F $?
Důkaz transformací KACHL ∝ SAT: pomocí proměnných $ x_{ijk} $, kde $ x_{ijk} = 1 $, pokud na pozici $ [i,j] $ se nachází kachlík typu $ k $. Jednotlivé klauzule se vytvoří tak, aby zaručovaly, že na každé pozici je právě jeden kachlík, že kachlíky navazují horizontálně, vertikálně i na kraje stěny.
3-SAT
Kubická CNF (vždy jen 3 proměnné v jedné disjunkci) $ F $ na $ n $ Booleovských proměnných. Existuje pravdivostní ohodnocení proměnných, které splňuje formuli $ F $?
Transformace SAT ∝ 3-SAT: stačí každou klauzuli (disjunkci) rozložit s pomocí nových volných proměnných na několik kubických klauzulí: $ (a_{i,1} \vee a_{i,2} \vee a_{i,3} \vee \dots \vee a_{i,k_i}) $ odpovídá $ (a_{i,1} \vee a_{i,2} \vee y_{i,1}) \wedge (\neg y_{i,1} \vee a_{i,3} \vee y_{i,2}) \wedge (\neg y_{i,2} \dots) \wedge \dots \wedge (\neg y_{i,k_i-3} \vee a_{i,k_i-1}\vee a_{i,k_i}) $
3-COLOR
Tříobarvení grafu: Mějme neorientovaný graf $ G=(V, E) $. Lze obarvit vrcholy ve $ V $ třemi barvami tak, aby žádná hrana v $ E $ neměla na obou koncích vrcholy stejné barvy?
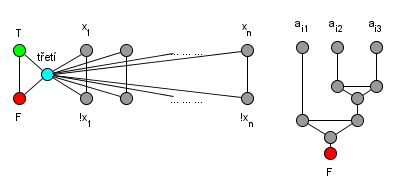
Transformace 3-SAT ∝ 3-COLOR: Vytvořím pro všechny proměnné a jejich negace vrcholy grafu a spojím se třemi body (z nichž každý musí být jinak barevný podle obrázku), aby proměnné musely mít barvu T nebo F. Proměnné a negace jsou taky spojené, aby bylo jednoznačně dána hodnota každé z nich. Pro každou klauzuli 3-SAT přidám grafík podle obrázku (napojím na proměnné, které představují literály klauzule a na druhé straně na barvu F), aby proměnné v něm nešly obarvit FFF.
KLIKA
Mějme neorientovaný graf $ G=(V, E) $ a přirozené číslo $ k $. Existuje $ V' \subseteq V $, $ |V’| = k $, indukující úplný podgraf grafu $ G $?
Transformace SAT ∝ KLIKA -- pro každý literál vytvořím bod grafu, spojím všechny body odpovídající literálům různých klauzulí, pokud se nejedná o komplementární proměnné, tj. mezi $ x_i $ a $ \neg x_i $ nevede hrana.
Nezávislá Množina (NM)
Mějme neorientovaný graf $ G=(V, E) $ a přirozené číslo $ q $. Existuje $ V' \subseteq V $, $ |V’| = q $, taková, že uvnitř $ V' $ nejsou žádné hrany?
Transformace KLIKA ∝ NM: stačí prohodit hrany a ne-hrany.
Vrcholové pokrytí (VP)
Máme neorientovaný graf $ G=(V, E) $ a přirozené číslo $ r $. Existuje $ V' \subseteq V $, $ |V’| = r $ taková, že každá hrana má ve $ V' $ alespoň jeden vrchol?
Transformace NM ∝ VP: NM je doplněk VP (vedou-li hrany do VP, už nemůžou vést mezi ostatními vrcholy).
Hamiltonovská Kružnice (HK)
Máme neorientovaný graf $ G=(V,E) $. Obsahuje G hamiltonovskou kružnici, tj. jednoduchou kružnici, která prochází každým vrcholem právě jednou?
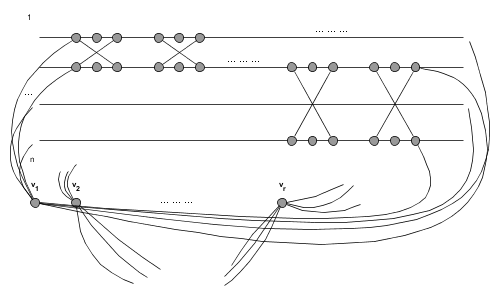
Transformace VP ∝ HK: Na $ |V| $ pomyslných linkách naskládám pro každou hranu původního grafu dvanáctici vrcholů spojených podle obrázku (widget). Krajní body všech linek spojím s vrcholy odpovídající původnímu VP $ v_1,\dots,v_r $. Protože widgety lze projít jen částečně (2x po linkách) nebo úplně (jednou všechny), bude HK vést částečným průchodem přes widgety, pokud oba vrcholy příslušné jejich hraně původního grafu patří do VP a úplným jinak.
Obchodní cestující (TSP)
Máme úplný neorientovaný graf $ G=(V,E) $, váhy $ w : E \to \mathbb{Z}_0^+ $ a číslo $ k \in \mathbb{Z}^+ $. Existuje v $ G $ hamiltonovská kružnice s celkovou váhou nejvýše $ k $? Někdy se počítá nad neúplným grafem a požaduje se hamiltonovský sled, tj. je možné opakovat vrcholy; to se ale na tuto definici snadno převede.
Transformace HK ∝ TSP: stačí nastavit váhy tak, že $ w(e) = 1 $, pokud $ e $ byla v původním grafu a $ w(e) = 2 $ jinak. Je-li chtěná váha rovna počtu vrcholů původního grafu, řešení dává HK v něm.
Součet podmnožiny (SP)
Jsou daná čísla $ a_1 , \dots ,a_n , b \in \mathbb{Z}^+ $. Existuje množina indexů $ S \subseteq \{1,\dots ,n\} $ taková, že $ \sum_{i\in S} a_i = b $?
Transformace VP ∝ SP: vyrobím incidenční matici grafu (řádky odp. vrcholům, sloupce hranám), kde budou jedničky na místech, kde daná hrana vede z daného vrcholu. Přidám k ní matici, jejíž řádky i sloupce odpovídají hranám a jedničky jsou pouze na diagonále (tj. každá hrana má jedničku ve "svém" řádku a sloupci). "Nalevo" od incidenční matice přidám sloupec plný jedniček. Řádky matice interpretuju jako čísla ve čtyřkové soustavě (v každém sloupci jsou tři jedničky, proto nedojde nikdy k přesunu řádů) a hledám součet podmnožiny jako číslo, které má na začátku velikost VP (sečte se ze sloupce jedniček) a následují samé dvojky (pro každou hranu).
Silná NP-úplnost, pseudopolynomiální algoritmy
Příklad
SP není exponenciální, ale polynomiální v počtu a velikosti čísel. Algoritmus (dynamické programování):
- Nechť $ a_1\leq a_2\leq \dots \leq a_n\,\! $ a $ A\,\! $ je bitové pole délky $ b\,\! $ (kde $ 1\,\! $ na pozici $ i\,\! $ bude indikovat možnost vytvoření podmnožiny se součtem $ i\,\! $).
- Všechny prvky pole $ A\,\! $ nastav na $ 0\,\! $ a $ a_0 $ nastav na b+1.
- Pro $ i\,\! $ od $ 1\,\! $ do $ n\,\! $ opakuj (hl. cyklus):
- $ A[a_i]:=1\,\! $
- Pro $ j\,\! $ od $ a_{i-1}\,\! $ do $ b\,\! $ zkoušej: když $ A[j] = 1\,\! $ a $ j+a_i\leq b\,\! $, nastav $ A[j+a_i]:=1\,\! $
- Je-li $ A[b] = 1\,\! $, podmnožina se součtem rovným $ b\,\! $ existuje.
Po $ i\,\! $-tém průchodu hlavním cyklem obsahuje $ A\,\! $ jedničky právě u všech součtů neprázdných podmnožin $ \{a_1,\dots,a_i\}\,\! $. Důkaz -- indukcí. Celk. složitost je $ O(n\cdot b)\,\! $, což je exponenciální vzhledem k binárně kódovanému vstupu, ale polynomiální, máme-li na vstupu čísla konstantní délky.
Definice (Pseudopolynomiální algoritmus)
Nechť je dán rozhodovací problém $ \Pi\,\! $ a jeho instance $ I\,\! $. Pak definujeme:
- kód(I) -- délka zápisu (počet bitů) instance $ I\,\! $ v binárním kódování (či jiném na něj polynomiálně převoditelném)
- max(I) -- velikost největšího čísla, vyskytujícího se v $ I\,\! $ (NE délka jeho binárního zápisu!)
Algoritmus se nazývá pseudopolynomiální, pokud je jeho časová složitost omezena polynomem v proměnných kód$ (I)\,\! $ a $ max(I)\,\! $. Každý polynomiální algoritmus je tím pádem pseudopolynomiální.
Poznámka (O číselných problémech)
Pokud pro nějaký problém $ \Pi\,\! $ platí, že $ \forall I:max(I)\leq p(\,\! $kód$ (I))\,\! $ pro nějaký polynom $ p\,\! $, pak všechny pseudopolynomiální algoritmy, řešící tento problém, jsou zároveň polynomiální.
Všechny problémy, kde tato rovnice neplatí(tj. neexistuje $ p\,\! $, že by platila), nazýváme číselné problémy.
Věta (O pseudopolynomialitě a NP)
Nechť $ \Pi\,\! $ je NP-úplný problém a není číselný. Pak pokud P$ \neq\,\! $NP, nemůže být $ \Pi\,\! $ řešen pseudopolynomiálním algoritmem.
Poznámka
Ani ne každý číselný problém je řešitelný pseudopolynomiálním algoritmem.
Věta (O pseudopolynomialitě a podproblémech)
Nechť $ \Pi\,\! $ je rozhodovací problém a $ p\,\! $ polynom. Potom $ \Pi_p\,\! $ označme množinu instancí (podproblém) problému $ \Pi\,\! $, pro které platí $ max(I)\leq p(\,\! $kód$ (I))\,\! $. Potom máme-li pseudopolynomiální algoritmus $ A\,\! $, který řeší problém $ \Pi\,\! $, určitě existuje polynomiální algoritmus, řešící $ \Pi_p\,\! $. Toto platí pro libovolné p.
Důkaz
Algoritmus $ A'\,\! $, řešící $ \Pi_p\,\! $ v polynomiálním čase, otestuje $ x\,\! $ na přítomnost v $ \Pi_p\,\! $ (spočítá kód$ (x)\,\! $ a $ max(x)\,\! $) a pokud $ x\in\Pi_p\,\! $, chová se stejně jako $ A\,\! $, takže běží v čase $ q(\,\! $kód$ (x),max(x))\leq q(\,\! $kód$ (x),p(\,\! $kód$ (x))) = q'(\,\! $kód$ (x))\,\! $.
Definice (Silně NP-úplný problém)
Rozhodovací problém $ \Pi\,\! $ je silně NP-úplný, pokud $ \Pi\in\,\! $NP a existuje polynom $ p\,\! $ takový, že podproblém $ \Pi_p\,\! $ je NP-úplný.
Věta (O silné NP-úplnosti)
Nechť problém $ \Pi\,\! $ je silně NP-úplný. Potom, pokud P$ \neq\,\! $NP, neexistuje pseudopolynomiální algoritmus, který by řešil $ \Pi\,\! $.
Důkaz
Plyne z předchozí věty.
Příklady
TSP je silně NP-úplný. Je to číselný problém, protože váhy hran nejsou omezené. Když váhy na hranách omezím, dostanu NP-úplný podproblém (jde na něj převést HK).
3-ROZDĚLENÍ je silně NP-úplné. Problém: máme $ a_1,\dots a_{3m},b\in \mathbb{N}\,\! $ takové, že $ \forall j:\frac{1}{4}b\leq a_j\leq\frac{1}{2}b\,\! $ a navíc $ \sum_{j=1}^{3m} a_j = mb\,\! $. Existuje $ S_1,\dots S_m\,\! $ disjunktní rozdělení množiny $ \{1,\dots,3m\}\,\! $ takové, že $ \forall i:\sum_{j\in S_i} a_j = b\,\! $?
Důkaz se provádí převodem z 3DM (třídimenzionální párování na tripartitních grafech), všechna čísla konstruovaná pro převod jsou polynomiálně velká vzhledem ke $ |G|\,\! $ (v převodu $ VP\propto SP\,\! $ byla exponenciálně velká).
Státnice -- Matematická lingvistika
Složitost a vyčíslitelnost -- Tvorba algoritmů, Odhady složitosti, NP-úplnost, Aproximační algoritmy, Vyčíslitelné funkce, Rekurzivní množiny, Nerozhodnutelné problémy, Věty o rekurzi.
Datové struktury -- Stromy, Hašování, Dynamizace, Vnější paměť, Třídění.
Formální popis jazyka -- Závislostní syntax, Frázové gramatiky, Obecná lingvistika, FGD, Formální sémantika
Statistické metody -- Korpusy, Strojové učení, Stochastické metody, Experimenty
Automatické zpracování jazyka -- Analýza jazyka, Generování jazyka, Analýza a syntéza řeči, Extrakce informací, Strojový překlad