Implementace databázových systémů/Indexace
okruhy 09/10 (pro srovnání): Metody indexace relací, datové struktury na externí pameti: hašování, B-stromy. Vícerozmerné dotazy pomocí hašovacích metod, vícerozmerných mrížek, vícerozmerných stromu. Prístupové metody k prostorovým objektum: R-stromy a jejich varianty. Vyhledávání v textech: indexy, signatury, metody implementace signatur (vrstvené kódování), usporádání odpovedí.
okruhy 14/15: Indexace relacních dat: B-stromy, hašování, GRACE algoritmus. Prístupové metody k prostorovým objektum: R-stromy a jejich varianty. Vyhledávání v textech: boolské a vektorové indexy a indexace, usporádání odpovedí, signatury a jejich implementace.
Obsah
Interní hašování
viz společná část "Hašování" dá se to přežít jenom s interním hashováním
Externí hašování
hashovací struktura se nevejde do hlavní paměti (RAM), efektivnost se počítá podle počtu přístupů k blokům v externí paměti (HDD)
Statické hashovací metody
- hashovací fce mapuje klíče do fixního počtu adres/stránek
- umožňují přidávat klíče ale neumožňují rozšiřovat adresní prostor bez přehashování celého indexu
- vhodné pro statické databáze
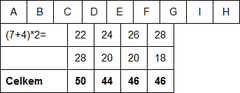
Cormack (perfektní hashování)
V vyzdvyhnutiu lubovolneho zaznamu su potrebne najviac dva pristupy na disk. Ak je adresar ulozeny v pamati tak potom jeden.
Potrebujeme:
- Hlavnu hashovaciu funkciu h(k) ktora vracia [0...n] Pre pristup k riadku adresara
- Pomocnu hashovaciu funkcia hᵢ(k, r) vracia hodnotu s ⟨0, r - 1⟩ napr hᵢ(k, r) = (k mod (2i + 100r + 1)) mod r
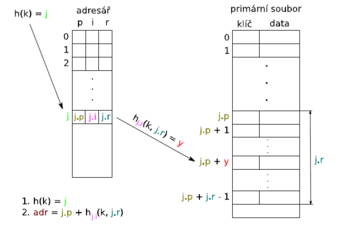
- Adresar ( Velkost O(n) kde n je velkost suboru ) ktory obsahuje parametre druhej hashovacej funkcie ( p : index do primarneho adresara, i index hashovacej funcie , r pocet miest na kolko hashovacia funcia hᵢ prvky hashuje)
- Primarny subor obsahuje data a je ulozeny na disku.
FIND: Pre pristup najprv vypocitame riadok s adresata funkciou h(k) = j . Adresa v hlavnom subore bude potom j.p + hⱼᵢ ( k, j.r )
INSERT: Vsetky hodnoty adresara su na zaciatku 0.
- Zistime riadok adresara
- Ak je prvy najdeme pre neho volne miesto , ulozime ho a zauktualizujeme adresar
- Ak nieje prvy zobereme kolidujuce zaznamy a pozrieme ci nemame koliziu. Ak nie najdeme novu funciu ktora bude mat obor hodnot tak aby sme zaheshovali n + 1 prvkov , najdeme volne miesto a zaktualizujeme adresar.
| Příklad |
|---|
Vysvetlivky:
p ... pointer do primarniho souboru
i ... index pouzite hashovaci funkce
r ... pocet kolidujicich prvku/rozsah pro hi (velikost bloku v prim.
souboru, jehoz zacatek dostanu pomoci has. fce h)
Hashovaci funkce:
h(k) = k mod 7
hi(k,r) = (k >> i) % r
Vkladane prvky:
8, 9, 23, 5, 12, 22, 2
i(8):
p i r
┌────┬───┬───┐ ┌────┐
0 │ │ │ │ 0 │ 8 │
1 │ 0 │ 0 │ 1 │ └────┘
2 │ │ │ │ \
3 │ │ │ │ primarni soubor
4 │ │ │ │
5 │ │ │ │
6 │ │ │ │ - adresar
└────┴───┴───┘
--------------------------------------------------------------------------
i(9):
p i r
┌────┬───┬───┐ ┌────┐
0 │ │ │ │ 0 │ 8 │
1 │ 0 │ 0 │ 1 │ 1 │ 9 │
2 │ 1 │ 0 │ 1 │ └────┘
3 │ │ │ │
4 │ │ │ │
5 │ │ │ │
6 │ │ │ │
└────┴───┴───┘
--------------------------------------------------------------------------
i(23):
23 % 7 = 2, dochazi ke kolizi. Najdeme nove misto v prim. souboru,
kam se vejdou oba kolidujici prvky (souvisly blok velikosti 2).
Prvni takovy existuje na pozici 2.
Zkusime pouzit fci h0:
23 % 2 = 1, ale take 9 % 2 = 1.
Musime tedy zvolit jinou hasovaci funkci.
Pouzijeme h1, vypocitame nove pozice prvku 9 a 23 v ramci bloku
velikosti 2.
(23 >> 1) % 2 = 11 % 2 = 1
(9 >> 1) % 2 = 4 % 2 = 0
Vysly ruzne hodnoty, tedy lze h1 pouzit.
p i r
┌────┬───┬───┐ ┌────┐
0 │ │ │ │ 0 │ 8 │
1 │ 0 │ 0 │ 1 │ 1 │ │
2 │ 2 │ 1 │ 2 │ 2 │ 9 │
3 │ │ │ │ 3 │ 23 │
4 │ │ │ │ └────┘
5 │ │ │ │
6 │ │ │ │
└────┴───┴───┘
--------------------------------------------------------------------------
i(5):
p i r
┌────┬───┬───┐ ┌────┐
0 │ │ │ │ 0 │ 8 │
1 │ 0 │ 0 │ 1 │ 1 │ 5 │
2 │ 2 │ 1 │ 2 │ 2 │ 9 │
3 │ │ │ │ 3 │ 23 │
4 │ │ │ │ └────┘
5 │ 1 │ 0 │ 1 │
6 │ │ │ │
└────┴───┴───┘
--------------------------------------------------------------------------
i(12):
Kolize s cislem 5. Zkusime pouzit hasovaci fci h0.
5 % 2 = 1
12 % 2 = 0
p i r
┌────┬───┬───┐ ┌────┐
0 │ │ │ │ 0 │ 8 │
1 │ 0 │ 0 │ 1 │ 1 │ │
2 │ 2 │ 1 │ 2 │ 2 │ 9 │
3 │ │ │ │ 3 │ 23 │
4 │ │ │ │ 4 │ 12 │
5 │ 4 │ 0 │ 2 │ 5 │ 5 │
6 │ │ │ │ └────┘
└────┴───┴───┘
--------------------------------------------------------------------------
i(22):
Kolize s 8. Fci h0 nelze pouzit k rozliseni, zkusime h1.
(8 >> 1) % 2 = 0
(22 >> 1) % 2 = 1
p i r
┌────┬───┬───┐ ┌────┐
0 │ │ │ │ 0 │ │
1 │ 6 │ 1 │ 2 │ 1 │ │
2 │ 2 │ 1 │ 2 │ 2 │ 9 │
3 │ │ │ │ 3 │ 23 │
4 │ │ │ │ 4 │ 12 │
5 │ 4 │ 0 │ 2 │ 5 │ 5 │
6 │ │ │ │ 6 │ 8 │
└────┴───┴───┘ 7 │ 22 │
└────┘
--------------------------------------------------------------------------
i(2):
Kolize s 9 a 23.
Fce h0 selze, protoze 23 % 3 = 2 % 3 = 2.
9 dec = 1001 bin
23 dec = 10111 bin
12 dec = 1100 bin
Zkusime h1:
(9 >> 1) % 3 = 4 % 3 =1
(23 >> 1) % 3 = 11 % 3 = 2
(2 >> 1) % 3 = 1
Zkusime h2:
(9 >> 2) % 3 = 2
(23 >> 2) % 3 = 2
(2 >> 2) % 3 = 0
Zkusime h3:
(9 >> 3) % 3 = 1
(23 >> 3) % 3 = 2
(2 >> 3) % 3 = 0
p i r
┌────┬───┬───┐ ┌────┐
0 │ │ │ │ 0 │ │ 8 │ 2 │
1 │ 6 │ 1 │ 2 │ 1 │ │ 9 │ 9 │
2 │ 8 │ 3 │ 3 │ 2 │ │ 10 │ 23 │
3 │ │ │ │ 3 │ │ └────┘
4 │ │ │ │ 4 │ 12 │
5 │ 4 │ 0 │ 2 │ 5 │ 5 │
6 │ │ │ │ 6 │ 8 │
└────┴───┴───┘ 7 │ 22 │
--------------------------------------------------------------------------
d(23):
Postupujeme podobne jako u vkladani. Potrebujeme najit souvisly blok
velikosti 2. Takovy je na zacatku, nemusime zvetsovat velikost
prim. souboru. Zmenime tedy p na 0. Snizime r a prozkousime has. fce.
Zkusime h0:
23 % 2 = 1
2 % 2 = 0
p i r
┌────┬───┬───┐ ┌────┐
0 │ │ │ │ 0 │ 2 │
1 │ 6 │ 1 │ 2 │ 1 │ 9 │
2 │ 0 │ 0 │ 2 │ 2 │ │
3 │ │ │ │ 3 │ │
4 │ │ │ │ 4 │ 12 │
5 │ 4 │ 0 │ 2 │ 5 │ 5 │
6 │ │ │ │ 6 │ 8 │
└────┴───┴───┘ 7 │ 22 │
└────┘
|
Dynamické hashovací metody
- umožňuje dynamický nárůst adresního prostoru pomocí dynamické hashovací fce
- vhodné pro db s měnící se velikostí
Fagin (rozšiřitelné adresářové hashování, Koubkovo "externí hashování")
Potrebujeme
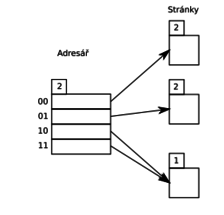
- Adresar ( Obsahuje ukazovatele / nie nutne unikatne / na stranky dat v na disku ; hlavicku v ktorej je ulozena hlbka adresara 0 < d < r) / aky pocet bitov sa bere s pseudokluca)
- Hashovaciu funkciu pre pseodukluc h(k). Pseodukluce maju vsetky rovnaku dlzku r
- Stranky na disku , stranka obsahuje lokalnu hlbku d`. Ak d` < d tak na jednu stranku vedie viac ukazovatelov
FIND:
- Spocitame pseodukluc k` = h(k)
- Vezmeme hlbku adresata (d) a precitame prvych d bitov s pseodokluca ( nazveme to p)
- Zobereme ukazovatel, ktory je umieneny v p.v ( v je velkost kazdeho pointra v bytoch ) ⇒ vedie na hladanu stranku
INSERT: Když se stránka naplní, rozštěpím ji na 2 podle dalšího bitu hash-funkce. Pokud už stránka používá stejně bitů jako adresář, musím zvětšit o 1 bit i adresář.
| Příklad |
|---|
Predpokladejme, ze do stranky se vejdou 2 zaznamy
h(k) = k mod 32 - hasovaci fce
-Vzdy na klic pouzijeme h(k) a potom vezmeme horni bity z takto
ziskaneho cisla.
-Pocet bitu, ktere budeme brat mame v "ousku" adresare. Pritom vzdy uvazujeme
vsech pet bitu z cisla, tj napr. 2 dec = 10 bin budeme uvazovat jako 00010
Vkladane hodnoty:
5, 20, 33, 28, 30, 8, 25
i(5): // 5 dec = 00101
"ousko" adresare - rika, kolik bitu ma adresar
┌─┐/ "ousko" u stranky - rika, kolik (hornich) bitu rozlisuje
│1└─┐ ┌─┐/ hodnoty
0 │ │─────│1└─┐
1 │ │─┐ │ 5 │
└───┘ │ │ │
│ └───┘
└┌─┐
│1└─┐
│ │
│ │
└───┘
i(20): // 20 dec = 10100
┌─┐
│1└─┐ ┌─┐
0 │ │─────│1└─┐
1 │ │─┐ │ 5│
└───┘ │ │ │
│ └───┘
└┌─┐
│1└─┐
│ 20│
│ │
└───┘
i(33): // 33 mod 32 = 1 = 00001
┌─┐
│1└─┐ ┌─┐
0 │ │─────│1└─┐
1 │ │─┐ │ 5│
└───┘ │ │ 33│
│ └───┘
└┌─┐
│1└─┐
│ 20│
│ │
└───┘
i(28): // 28 = 11100
┌─┐
│1└─┐ ┌─┐
0 │ │─────│1└─┐
1 │ │─┐ │ 5│
└───┘ │ │ 33│
│ └───┘
└┌─┐
│1└─┐
│ 20│
│ 28│
└───┘
i(30): // 30 = 11110
Chceme umistit hodnotu do stranky, ktera je plna. Zvetsime adresar, po zmene
bude dvoubitovy. Strankam, ktere nepotrebujeme stepit jen zvetsime "rozsah",
prvky ze stepenych stranek rozhazime podle hornich bitu do spravnych stranek.
Take si do "ouska" stranek poznamename, ze rozlisujeme hodnoty podle dvou
bitu.
┌─┐ ┌─┐
│2└─┐ │1└─┐
00 │ │─┬───│ 5│
01 │ │─┘ │ 33│
10 │ │───┐ └───┘
11 │ │─┐ └─────┌─┐
└───┘ └┌─┐ │2└─┐
│2└─┐ │ 20│
│ 28│ │ │
│ 30│ └───┘
└───┘
i(8): // 8 = 01000
Vkladame do plne stranky, ta se ale da rozstepit, protoze rozlisuje
hodnoty jen podle jednoho bitu.
┌──────────┌─┐
┌─┐ │ ┌─┐ │2└─┐
│2└─┐│ │2└─┐ │ 5│
00 │ │┘┌───│ 8│ │ 33│
01 │ │─┘ │ │ └───┘
10 │ │───┐ └───┘
11 │ │─┐ └─────┌─┐
└───┘ └┌─┐ │2└─┐
│2└─┐ │ 20│
│ 28│ │ │
│ 30│ └───┘
└───┘
i(25): // 25 = 11001
Vkladame do plne stranky, jeji "rozsah" nelze rozdelit (rozlisuje hodnoty
podle dvou bitu) - musime zvetsit adresar a rozdelit prislusnou stranku a
zmenit "rozsahy" jednotlivych stranek.
┌─────────┌─┐
┌─┐ │ ┌─┐ │2└─┐
│3└─┐ │ │2└─┐ │ 8│
000 │ │─┤┌──│ 5│ │ │
001 │ │─┘│ │ 33│ └───┘
010 │ │─┬┘ └───┘
011 │ │─┘ ┌─┐
100 │ │─┬────────────│2└─┐
101 │ │─┘ ┌─┐ │ 20│
110 │ │─────────│3└─┐│ │
111 │ │──┌─┐ │ 25│└───┘
└───┘ │3└─┐ │ │
│ 28│ └───┘
│ 30│
└───┘
|
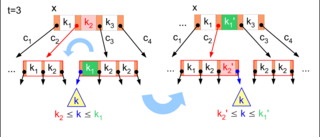
Litwin (lineární bezadresářové hashování)
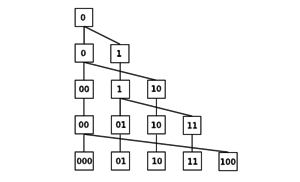
Nevyužívá adresář, ale potřebuje oblast přetečení a tedy není zaručeno, že se ke všem datům dostaneme v 1 přístupu na disk. Data uložena ve stránkách.
Stránky jsou štěpeny nezávisle na tom, kde došlo ke kolizi, kruhovým schématem (viz obrázek). Po každých L (L je parametr metody) vloženích je rozštěpena 1 stránka. Když dochází ke štěpení stránky, přidáme 1 stránku na konec úložiště stránek . Záznamy ze štěpené stránky (a případné z oblasti přetečení, které by patřily do štěpené stránky) jsou potom rozděleny mezi novou a štěpenou stránku.
FIND: h(k) = k` (pseudoklíč má na rozdíl Fagina podle posledních bitů a jeho délku spočítá podle počtu všech stránek, pokud tam není hledáme v obl.přetečení)
INSERT: najdi místo pomocí FIND a pak vložíme, pokud se nevejde tak nacpeme do oblasti přetečení, po L INSERTech štěpíme a podle posledních bitů rozdělíme záznamy
Růst primárního souboru je lineární ⇒ lineární hashování
| Příklad |
|---|
Hasovaci fce - v nasem pripade pouze prevod z desitkove do dvojkove soustavy
Vysvetlivky:
b = 3 ...velikost bloku
l = 2 ...po kolika insertech se ma stepit stranka
Vkladane hodnoty:
12, 5, 4, 1, 3, 2, 7, 14
i(12):
┌────┐ Kdyz mame jedinou stranku (do 1. stepeni), vkladame do ni
│ 12 │ vsechny hodnoty (nezalezi na poslednim bitu).
│ │
│ │
└────┘
i(5):
┌────┐
│ 12 │
│ 5 │
│ │
└────┘ "oznaceni stranky" - posledni bit(y) cisel ve strance maji
├──────┐ / tuto hodnotu
│ 0 │ 1
┌────┐ ┌────┐ Protoze l=2 a vlozili jsme druhy prvek, dojde ke stepeni.
│ 12 │ │ 5 │ Podle posledniho bitu cisel se rozhodne, do
│ │ │ │ ktere pujdou stranky.
│ │ │ │
└────┘ └────┘
i(4):
0 1
┌────┐ ┌────┐
│ 12 │ │ 5 │
│ 4 │ │ │
│ │ │ │
└────┘ └────┘
i(1):
0 1
┌────┐ ┌────┐
│ 12 │ │ 5 │
│ 4 │ │ 1 │
│ │ │ │
└────┘ └────┘
├──────────────┐
│ 00 1 │10
┌────┐ ┌────┐ ┌────┐ Vlozili jsme 4. prvek - dochazi ke stepeni.
│ 12 │ │ 5 │ │ │ Hodnoty rozdelujeme podle poslednich dvou
│ 4 │ │ 1 │ │ │ bitu.
│ │ │ │ │ │
└────┘ └────┘ └────┘
i(3):
00 1 10
┌────┐ ┌────┐ ┌────┐
│ 12 │ │ 5 │ │ │
│ 4 │ │ 1 │ │ │
│ │ │ 3 │ │ │
└────┘ └────┘ └────┘
i(2):
00 1 10
┌────┐ ┌────┐ ┌────┐
│ 12 │ │ 5 │ │ 2 │
│ 4 │ │ 1 │ │ │
│ │ │ 3 │ │ │
└────┘ └────┘ └────┘
├──────────────┐
00 │ 01 10 │11
┌────┐ ┌────┐ ┌────┐ ┌────┐
│ 12 │ │ 5 │ │ 2 │ │ 3 │
│ 4 │ │ 1 │ │ │ │ │
│ │ │ │ │ │ │ │
└────┘ └────┘ └────┘ └────┘
i(7):
00 01 10 11
┌────┐ ┌────┐ ┌────┐ ┌────┐
│ 12 │ │ 5 │ │ 2 │ │ 3 │
│ 4 │ │ 1 │ │ │ │ 7 │
│ │ │ │ │ │ │ │
└────┘ └────┘ └────┘ └────┘
i(14):
00 01 10 11
┌────┐ ┌────┐ ┌────┐ ┌────┐
│ 12 │ │ 5 │ │ 2 │ │ 3 │
│ 4 │ │ 1 │ │ 14 │ │ 7 │
│ │ │ │ │ │ │ │
└────┘ └────┘ └────┘ └────┘
├───────────────────────────┐
│000 01 10 11 │100
┌────┐ ┌────┐ ┌────┐ ┌────┐ ┌────┐
│ │ │ 5 │ │ 2 │ │ 3 │ │ 12 │
│ │ │ 1 │ │ 14 │ │ 7 │ │ 4 │
│ │ │ │ │ │ │ │ │ │
└────┘ └────┘ └────┘ └────┘ └────┘
|
| další zdroje |
|---|
|
https://is.cuni.cz/webapps/zzp/detail/46740/
|
GRACE algoritmus
viz Algoritmy implementace relacních operací.
B-stromy (🎓🎓🎓🎓)
| praktické použití B-stromů: |
|---|
|
- Více I2 praktický pohled z OZD - důležitá otázka pro databázisty
- okruhy 14/15: B-stromy a jejich varianty
| Zážitky ze zkoušek |
|---|
|
- umožňují při daném klíči najít záznam pomocí několika málo operací, na rozdíl od hashování ale i klíče z nějakého intervalu
- nejčastější pro indexy na externí paměti, pomocí "klastrování" odfiltrujeme nerelevantní záznamy
B-strom (redundantni, neredundantni)
- setříděný vyvážený m-nární strom s definovanými omezeními větvení (díky nim je rozumně široký)
💡 inserty a delety způsobují pouze lokální změny
pravidla pro neredundatní verzi:
- kořen má ≥2 syny (pokud není list)
- ∀vnitřní uzel (mimo kořene) má od ⌈m/2⌉ do m synů
- ∀uzel má od ⌈m/2⌉-1 do m-1 (poiterů na) datových záznamů
- ∀větev má stejnou délku
- uzly vypadají takhle: p₀,(k₁,p₁,d₁),(k₂,p₂,d₂), ... ,(kₙ,pₙ,dₙ),u (p - pointery, k - klíče - řadí se podle nich, d - data/pointery na data)
- podstromy mají hodnoty klíče mezi klíči z otce
💡 v neredundatních se teoreticky dostaneme rychleji k záznamům (ve vnitřních uzlech)
redundatní - mají datové záznamy pouze v listech, takže klíče jsou redundantní ve vnitřních uzlech
- Implementace
💡 většinou 1 stránka/blok(8kb) = 1 uzel , tedy arita B-Stromu je okolo 500 a výška se drží okolo 3
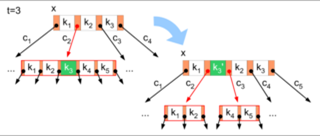
- INSERT
- najdeme list kam vložit a pokud je plný uděláme split takže každý nový list je z půlky plný
- split můžeme zvýšit počet podstromů otce ⇒ split kaskáda (💡 možná optimalizace: přetékáme do sousedů = vyvažování stránek ⇒ nenastane kaskáda)
- DELETE
- pokud je po delete uzel méně než z pulky plný mergujeme se sousedem
- merge můžeme snížit počet podstromů otce ⇒ merge kaskáda
Oba algoritmy pracují v O(log N) v nejhorším případě.
B+-stromy (redundantni)
tedy data (pointry na ně) jsou pouze v listech, a listy jsou propojeny pointery (💡 nelistové vyšší úrovně mouhou být také propojeny - např. MSSQL pro intervalové zámky)
- menší vnitřní uzly ⇒ nižší výška (pže uzly mohou být větší) a tj.rychlejší hledání
- INSERT/DELETE jednodušší ⇒ jednodušší implementace (hlavně range queries)
B*-strom (redundantni, neredundantni)
generalizace vyvažování:
- kořen má ≥2 syny (pokud není list)
- ∀větev má stejnou délku
- ∀uzel má alespoň ⌈(2m-1)/3⌉ synů
- INSERT/DELETE
- Štěpení se odkládá, dokud nejsou sourozenci plní, potom se štěpí buď 2 do 3. Při odebírání se slévají 3 uzly do 2.
💡 detailněji zde: B-Stromy
| staré |
|---|
;Vícerozměrné B-stromy
Jiny (urcite lepsi :) popis:
Definice: Klíč schématu relace R je nejmensi mnozina atributů ze schématu R, na níz celá R funkčně závisí. Jakmile tedy máme hodnoty pro klíčové atributy, máme jednoznačné určen libovolný řádek tabulky.
|
Přístupové metody k prostorovým objektům: R-stromy a jejich varianty (🎓🎓🎓)
| Zážitky ze zkoušek |
|---|
|
Typické dotazy na prostorová data jsou:
- vyhledej bod v prostoru
- vyhledej oblast v prostoru
- vyhledej okolí oblasti (bodu)
R-stromy
💡 obdoba B-stromů pro prostorové objekty (ale hledání může jít současně více cestami)
- ∀uzel E má m až M synů (až na kořen - má aspoň 2 syny) a platí: m ≤ M/2
- E.p - identifikátor prostorového objektu (listy) nebo pointer na syna
- E.I - MBR (minimum bounding rectangle) - minimální ohraničující obdélník (MOO)
- 💡 n-dimensionální: MBB (minimum bounding box) - minimální ohraničující kostka (MOK)
- 💡 jednotlivé oblasti se mohou překrývat
- všechny cesty v R-stromu jsou stejně dlouhé (listy na stejné úrovni) ≤ logₘ n
INSERT - štěpení uzlu při jeho M+1 přeplnění (hledám co nejmenší využití prostoru)
Guttman (kvadratická verze, lin.dává horší výsledky)
- PickSeeds - vybrat dvojici prvků s největší nevyužitou plochou
- 💡 napáchaly by největší škodu, pokud bychom je dali do stejné skupiny
- ∀(zbývající uzel) PickNext - postupně k nim přiřazujeme zbylé prvky aby přírustek nev.plochy byl co nejmenší
- |přírustek k původnímu MBR 1.skupiny pomocí dalšího uzlu - přírustek pův. MBR 2.skupiny pomocí stejného uzlu|
- vybereme maximální rozdíl (💡 tj.přidání do op. skupiny by napáchalo největší škodu)
Greenová (snažíme se odstranit překrytí listů - při štěpení vyberem jednu z os)
ChooseAxis (=modifikace Guttmana)
- PickSeeds - z Guttmana
- ∀ osu a MBR(2 prvků) spočti maximální normalizovanou vzdálenost (💡 vnitřní vzdálenost vydělím hranou MBR 2 prvků v dané ose)
- → vyberu osu s největší normalizovanou vzdáleností
- Distribute - větší půlka ⌈(M+1)/2⌉ se hodí do jednoho uzlu a zbytek do druhého uzlu.
- 💡 ne vždy je nalezena vhodná osa – může vést ke špatným výsledkům
R+-stromy
- vnitřní (nelistové) MBR uzly se nepřekrývají ⇒ měně větvení dotazu ALE více dělení a větší výška než R-Stromy
- přiřazuje prostorové objekty do všech listů, do kterých zasahují (tj. odkaz na objekt duplikován)
- u uzlů není zaručena minimální zaplněnost
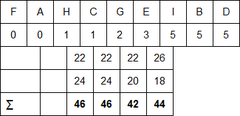
R*-stromy
- více optimalizačních kritérií oproti R-stromům – minimalizují pokrytí a překrytí pomocí okraje
- rozdíl od R-Stromů: algoritmem na rozdělení přetečené stránky, bere v úvahu více trideni podle os, při přetečení provádí reinsertování, taky algoritmem na hledání listu pro insert (overlap místo nejmenšího rozšíření)
- při INSERTu se v předposlední úrovni vybírá takový list, kde když bude, tak celá ta množina bude mít nejmenší překrytí s ostatními množinami (dalšími listy), ve vyšších úrovních se vybírá uzel, který způsobí nejmenší zvětšení prostoru (jako u R-stromů)
- Split_RS - štěpení
- prvky se setřídí do 2 skupin podle osy x1 a x2
- ∀setřídění jsou vytvořeny všechny kombinace rozdělení prvků tak, aby v 1. skupině bylo aspoň (m-1)+k prvků
- ChooseSplitAxis - ∀osu se dle ní setřídí prvky a spočítá suma margin-value všech distribucí v dané ose a vybere se osa s nejmenší (margin-value sumou)
- ChooseSplitIndex - v této ose se vybere distribuce s nejmenší overlap-value, pokud se rovnají menší area-value
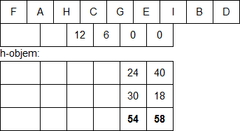
- area-value (h-objem) - součet obou MBR distribucí
- margin-value (h-okraj) - součet okrajů – ve 2D obvod MBR, ve 3D ohraničující plocha MBB distribucí
- overlap-value (h-překrytí) - překrytí obou MBR distribucí
- rozdělíme prvky do 2 distribucí
- prvky se setřídí do 2 skupin podle osy x1 a x2
- Forced Reinsert
- ∀prvky nodu N sestupně setřid podle vzd. od středu MBR
- prvních p prvků odstraň z N a pak je znova insertuj
| další stromy |
|---|
další:
|
| další zdroje |
|---|
|
Vyhledávání v textech: boolské a vektorové indexy a indexace, usporádání odpovedí, signatury a jejich implementace (🎓)
| Zážitky ze zkoušek |
|---|
|