Státnice - Algoritmicky vyčíslitelné funkce, rekurzivní a rekurzivně spočetné množiny
Ze zápisků k zkoušce z ZSV , maly uvod pokud jste toho uz hodne zapomneli: pohadky vycislitelnost
09/10, 14/15: Algoritmicky vycíslitelné funkce, jejich vlastnosti, ekvivalence jejich ruzných matematických definic. Cástecne rekurzivní funkce. Rekurzivní a rekurzivne spocetné množiny a jejich vlastnosti.
Obsah
Algoritmicky vyčíslitelné funkce, jejich vlastnosti, ekvivalence jejich různých matematických definic. Částečně rekurzivní funkce. (4×🎓)[editovat | editovat zdroj]
| Zážitky ze zkoušek |
|---|
|
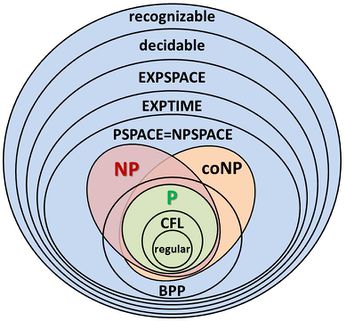
💡 efektivně vyčíslitelné = turingovsky vyčíslitelné = algoritmicky vyčíslitelné = algoritmicky řešitelné
PRF, ČRF, RP, RSP a vlast.[editovat | editovat zdroj]
💡 Behold - Ultimate Table of Life, the Universe, and Everything!
| fce | predikát | množina | problém | ||||||
|---|---|---|---|---|---|---|---|---|---|
| odvozeny pomocí | vlastnosti | ∃ pro něj (odp.)char.fce | vlastnosti | je def.oborem (odp.)fce je (odp.)unárním predikátem |
vlastnosti | ||||
| PRF | Základní fce:
Operátory:
|
Uzavřenost:
|
PRP | χP(x⃗ ) ≃ 1 pro R(x⃗ ) jinak ≃0 |
Uzavřenost:
|
nezavádí se | |||
| ORF | ČRF def.∀vstupy (totální) | ORP | χP(x⃗ ) ≃ 1 pro R(x⃗ )
jinak ≃0 (jako PRP) |
RM | χA(x)↓= 1 pro x∈A jinak χA(x)↓= 0 |
Uzavřenost:
Generování RM:
|
rozhodnutelný
(decidable) | ||
| ČRF | Nový operátor:
|
|
RSP | Částečná char.fce: χR(x⃗ )↓ pro R(x⃗ ) jinak χR(x⃗ )↑ |
Uzavřenost:
|
RSM | χA(x)↓ pro x∈A jinak χA(x)↑ |
Uzavřenost:
Generování RSM:
Převoditelnost:
|
částečně rozhodnutelný (recognizable) |
| minimalizace $ M_n(f) = h $
|
|---|
|
podmíněná rovnost f(x₁, .., xₙ) ≃ g(x₁, .., xₙ) znamená: hodnota f(x₁, .., xₙ) je definována ⇔ definována i hodnota g(x₁, .., xₙ), a pak jsou si také rovny
Základní funkce:
- nulová (konstantní) funkce o(x) = 0
- následník s(x) = x + 1
- projekce Iₙʲ (x₁, .., xⱼ, .. , xₙ) = xⱼ (💡 vrací hodnotu j-tého parametru)
Operátory: ( x = (x₁, .., xₙ) )
- substituce Sₙᵐ(f, g₁,..., gₘ) = h kde: h(x₁, .., xₙ) ≃ f(g₁(x₁, .., xₙ),..., gₘ(x₁, .., xₙ))
- 💡 f má m proměnných a g₁, .. , gₘ n proměnných
- 💡 Operátor substituce je základní prvek programování — jednoduše úlohu, kterou mám řešit, vyřeším pomocí funkcí, které už naprogramoval někdo dřív.
- primitivní rekurze Rₙ(f, g) = h
- kde: h(0, x₂, ..., xₙ) ≃ f(x₂, ..., xₙ)
- h(i + 1, x₂, ..., xₙ) ≃ g(i, h(i , x₂, ..., xₙ), x₂, ..., xₙ)
- 💡 f je fce n - 1 proměnných a fce g n + 1 proměnných (n ≥ 2)
- 💡 operátor primitivní rekurze má sílu for-cyklu.
- 💡 Proměnná x₁ nebo i má zvláštní význam — slouží jako čítač
- kde: h(0, x₂, ..., xₙ) ≃ f(x₂, ..., xₙ)
- minimalizace Mₙ(f) = h (má sílu while-cyklu)
- h(x₁, .., xₙ)↓ ≃ min { y | f(x₁, .., xₙ, y)↓ = 0 a ∀z < y : f(x₁, .., xₙ, z)↓ ≠ 0 }
- μy[P(x, y)] - fce μ vrátí nejmenší y takové, aby platil predikát P(x, y)
- 💡 lze jí sestrojit pomocí operátoru minimalizace
- μy[P(x, y)] - fce μ vrátí nejmenší y takové, aby platil predikát P(x, y)
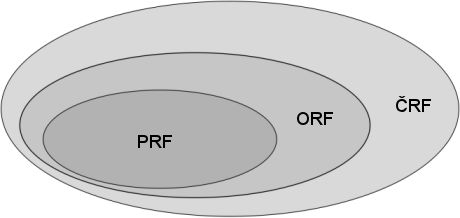
PRF ⇐ lze odvodit ze 3 základních fcí a pomocí 2 op. substituce a prim. rekurze (NE minimalizace)
- 💡 všude definována (=totální) - for-cykly (vždy konvergují)
- 💡 PRF je ORF bez minimalizace
- PRP ⇐ ∃ pro něj PRF charakteristická funkce
- predikát R(x₁, .., xₙ) je relace nebo libovolný fakt o n proměnných
- charakteristická fce predikátu R je χP(x₁, .., xₙ) ≃ 1 pro R(x₁, .., xₙ) jinak ≃0
- 💡 char. fce je ORF
- 💡 (Obecně) PRM je unární (obecně) PRP.
- charakteristická fce predikátu R je χP(x₁, .., xₙ) ≃ 1 pro R(x₁, .., xₙ) jinak ≃0
- predikát R(x₁, .., xₙ) je relace nebo libovolný fakt o n proměnných
ČRF (partial μ-recursive functions) ⇐ lze odvodit ze 3 základních funkcí pomocí 3 operátorů (💡 mají navíc while-cyklus ⇒ divergence)
- ORF - je ČRF def. pro ∀ vstupy (totální)
- ORP ⇐ ∃ pro něj ORF charakteristická funkce
- RSP ⇐ ∃ pro něj ČRF charakteristická funkce
- částečná char. fce (=ČRF) predikátu R je funkce fR: ℕⁿ → ℕ : fR(x₁, ... , xₙ)↓ ⇔ R(x₁, ... , xₙ), ∀(x₁, ... , xₙ) ∈ ℕ.
- 💡 je def.oborem nějaké ČRF
Jejich základní vlastnosti[editovat | editovat zdroj]
- (uzavřenost na aritm.operace: konečný + a ×) f je PRF 2 proměnných ⇒ je PRF i:
- g(z, x) = ∑y<z f (y, x) ( přičemž g(0, x) = 0 )
- h(z, x) = ∏y<z f (y, x) ( přičemž h(0, x) = 1 )
- 💡 analogicky i pro PRF 1 proměnné (tj. vyhodíme všude x)
- (podmíněný příkaz) - analogie switch/case/if-then
- g₁,..., gₙ , jsou PRF a R₁(x), ..., Rₙ(x) jsou PRP a ∀x ∈ ℕ je splněn !1 z nich.
- ⇒ tato fce f je PRF: $ \begin{align} f(x)=g_1(x)&\Leftrightarrow R_1(x)\\ f(x)=g_2(x)&\Leftrightarrow R_2(x)\\ &\vdots&\\ f(x)=g_n(x)&\Leftrightarrow R_n(x) \end{align} $
- kvantifikátory (omezené i neomezené).
- (omezená kvantifikace) $ P $ binární PRP ⇒ $ V_P(z, x)=(\forall y<z)[P(y, x)] $ a $ E_P(z, x)=(\exists y<z)[P(y, x)] $ jsou PRP.
- (neomezená kvantifikace): P unární PRP⇒ (∃y)[P(y)] je RSP a (∀y)[P(y)] je doplněk RSP (∃y)[¬P (y)].
- (ne)uzavřenost na logické spojky
- (logické spojky)
- $ P $ a $ R $ unární PRP ⇒ $ R\wedge P $, $ R\vee P $ a $ \neg P $ jsou PRP
- (konečná konjunkce a disjunkce)
- $ P $ binární PRP ⇒ $ A(x, z)=\bigwedge_{y<z}P(x, y) $ a $ B(x, z)=\bigvee_{y<z}P(x, y) $ jsou PRP
- (omezená minimalizace)
- $ P $ binární PRP ⇒ tato $ f $ je PRF:
- $ f(x, z)= \begin{cases} \min\{y<z\;|\;P(x, y)\} \quad &\mbox{pokud takové y existuje}\\ z \quad &\mbox{jinak.} \end{cases} $
- Funkci $ f $ budeme také označovat pomocí $ f(x, z)=\mu y<z[P(x, y)] $.
Ekvivalence jejich definic (ČRF ⇔ TS)[editovat | editovat zdroj]
Věta ( ČRF ⇒ TS ): $ h $ je ČRF $ n $ proměnných ⇒ $ h $ je Turingovsky vyčíslitelná
| Dk (konstrukcí TS, zde komplet včetně nižší úrovně) |
|---|
:💡 Věta přesněji: existuje Turingův stroj $ M_h $ takový, že pro každou $ n $-tici přirozených čísel $ x_1, x_2, \dots, x_n $ platí
Věta ( 💡 ): Převod je navíc možno učinit efektivně. Jinými slovy, existuje Turingův stroj CRF2TS, který pokud na vstupu dostane kód ČRF $ h $, spočítá Gödelovo číslo $ e $ stroje $ M_e $, který počítá funkci $ h $. |
Věta ( TS ⇒ ČRF ): funkce $ f $ turingovsky vyčíslitelná ⇒ je $ f $ ČRF
| Dk (jeden krok TS je PR - omezené cykly, TS pracuje, dokud neskončí = while-cyklus (tj. minimalizace), tedy program = minimalizace čehosi, kde to cosi už je PR) |
|---|
* předpoklady: f je def. jako tur. vyčíslitelná ⇒ ∃ TS $ M_e $ co jí počítá (💡 to je z definice tur.vyčíslitelnosti)
Tato část je neúplná a potřebuje rozšířit. jak se to dělá?
|
Rekurzivní a rekurzivně spočetné množiny a jejich vlastnosti. (4×🎓)[editovat | editovat zdroj]
| Zážitky ze zkoušek |
|---|
|
charakteristická funkce χA(x) -- charakteristická fce predikátu náležení do množiny ( χA(x)↓= 1 pro x ∈ A a jinak χA(x)↓= 0 )
$ χ_A(x_1,\dots,x_n)\simeq \begin{cases}1 \quad & \mbox{ pokud } R(x_1,\dots,x_n) \\ 0 \quad & \mbox{ jinak }\end{cases}\,\! $
- 💡 částečná charakteristická funkce množiny -- χA(x)↓= 1 pro x ∈ A a jinak χA(x)↑
dom značí definiční obor, rng obor hodnot
RM A ⊆ ℕ ⇐ je-li charakteristická funkce χA(x) ORF
- 💡 také nazýváme jako unární RP (příklad: binarni predikat je mnozina dvojic, ale unarni predikat je mnozina prvku)
RSM A ⊆ ℕ ⇐ je-li def. oborem ČRF
- 💡 také nazýváme jako unární RSP
- 💡 tj: A = dom ČRF f = { x | f(x)↓ }
- e-tá RSM $ \mathbf{W_e} = dom~ φ_e = \{ x | φ_e(x)↓ \} $
- Pomocí $ \varphi^{(n)}_{e, s} $, kde $ e, n,s\in{\mathbb N} $ označíme konečnou aproximaci $ \varphi_{e, s}^{(n)} $ funkce $ \varphi_e^{(n)} $, kterou definujeme následujícím způsobem:
- $ \varphi^{(n)}_{e, s}(x_1, \dots, x_n)\simeq \begin{cases} \varphi^{(n)}_e(x_1, \dots, x_n) \quad & \mbox{pokud }(\exists y<s)[T_n(e, x_1, \dots, x_n, y)]\\ \uparrow\quad & jinak \end{cases} $
- rekurzivní konečná aproximace $ \mathbf{W_{e,s}} = dom φ_{e,s} = \{ x | φ_{e,s}(x)↓ \} $
Věta ( RM - uzavřenost na ∪, ∩ a doplňek ): RM jsou uzavřeny na sjednocení, průnik a operaci doplňku
| Dk: |
|---|
předpokládáme, že signum, součet, součin a opatrné odčítání 1 (predecessor) jsou PRF/ORF :
|
Věta ( RSM - uzavřenost na ∪, ∩ ale NE na doplňek ): Rekurzivně spočetné množiny jsou efektivně uzavřené na sjednocení a průnik, nikoliv na doplněk.
| Dk: |
|---|
: A∪B - pustíme oba TS současně a když 1 skončí vstup patří do sjednocení
|
| Postova věta v kontextu množin |
|---|
| Věta ( Postova věta v kontextu množin ): $ A $ je RM $ \Leftrightarrow A $ i $ \overline A={\mathbb N}\setminus A $ jsou RSM
|
| predikáty RSP,... |
|---|
| Lemma : Predikát $ H $ definovaný jako $ H (e, s, x_1, . . , x_n) ⇔ φ_{e,s}(n)(x_1, . . , x_n)↓ $ je PRP a platí, že: $ φ_e(n) (x_1, . . . , x_n)↓⇔ (∃s)[ φ_{e,s}(n) (x_1, . . , x_n)↓] $ . (v dk předpokladáme, že $ T_n $ z Kleenovy věty je PRP a omezená kvantifikace je PR.) Kódování uspořádaných dvojic, n-tic:
Věta ( důsledek Kleeneho věty ): Predikát $ R ⊆ N^n $ je RSP ⇔ ∃ PRP $ P ⊆ N^{n+1} $ , že: $ R(x_1, . . , x_n) ⇔ (∃y)[P (x_1, . . , x_n, y)] $. Věta ( RSP jsou uzavřeny na ∃ kvantifikátor ): $ P(x_1, \dots, x_n, y) $ je RSP ⇒ $ R(x_1, \dots, x_n)=(\exists y)\;[P(x_1, \dots, x_n, y)] $ je RSP
Věta ( výběrová funkce ): $ R(x, y) $ je RSP ⇒ $ \exists $ ČRF $ f $ (také výběrová funkce nebo selektor pro $ R $), že $ f(x)\downarrow\Leftrightarrow(\exists y)R(x, y) $ a pokud $ f(x)\downarrow $, pak $ R(x, f(x)) $. 💡 $ \exists f $ implementující $ \exists y $ na predikátu $ R(x, y) $
|
| další zdroje |
|---|
|
|
RM = rng rost. úsekové ČRF[editovat | editovat zdroj]
$ f $ je úseková fce, pokud její definiční obor tvoří počáteční úsek $ \mathbb N\,\! $
Věta ( $ RM = rng $ rostoucí úsekové ČRF ): A je RM $ \Leftrightarrow $ je oborem hodnot nějaké rostoucí úsekové ČRF
| Dk (oběma směry - neformálně, zde formálnější přepis ze skript) |
|---|
$ \Rightarrow\,\! $: Předpokládejme nejprve, že $ A $ je RM. Zkonstruujeme rostoucí, úsekovou ČRF $ f(i) $ = "vrať $ i $-tý nejmenší prvek z $ A $".
$ \Leftarrow\,\! $: Nyní předpokládejme, že $ A = rng f $, kde $ f\,\! $ je rostoucí úsekovou ČRF.
|
💡 Důsledek: Nechť $ A $ je ∞ množina: $ A $ je $ RM ⇔ A=rng $ nějaké rostoucí ORF. (protože úsekové funkce s nekonečnou doménou musí být všude definované = totální)
RSM = rng ORF, či ČRF[editovat | editovat zdroj]
| Zážitky ze zkoušek |
|---|
|
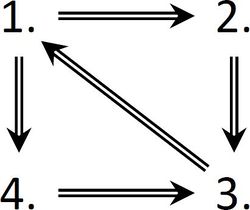
Věta ( Generování RSM ): Následující tvrzení jsou ekvivalentní:
- A je RSM.
- A je ∅, nebo je $ rng $ nějaké ORF
- A je $ rng $ nějaké ČRF.
- A je $ rng $ nějaké rostoucí ČRF.
| Dk (neformální, zde komplet) |
|---|
|
$ 1. ⇒ 2. $ (konstrukce ORF co pro jakékoli vstupy vrací prvky z A):
Každý prvek $ W_e $ je tedy funkcí $ g $ pro nějaký vstup $ y $ vrácen, jenom nedokážeme odhadnout, pro jak velké $ y $. Dohromady dostáváme, že $ A = W_e = rng~ g $. $ 2. ⇒ 3. $ : Plyne z toho, že každá ORF je i ČRF. ∅ je oborem hodnot ČRF, která není definovaná pro žádný vstup. $ 3. ⇒ 1. $ (pomocí částečné aproximace vyrobíme z ČRF RSP => RSM): Předpokládejme, že $ A $ je oborem hodnot ČRF $ g ≃ φ_e $.
$ 1. ⇒ 4. $ (zkonstruujeme triviální rostoucí ČRF $ h(x)=g(e,x) $ u které se $ dom $=$ rng $) : Předpokládejme, že $ A = W_e $, tedy $ A = dom φ_e $. Buď $ g(e, x) $ fce definovaná jako:
$ 4. ⇒ 3. $ : Toto je zřejmé. Implikaci $ (3. ⇒ 1.) $ už máme hotovou. Tato část je neúplná a potřebuje rozšířit. {{{1}}}
1=>3
1<=3
|
≤1, ≤m, K a K0 1-úplné, RSM a ¬RM.[editovat | editovat zdroj]
A ≤ₘ B (množina A je m-převoditelná na B) pokud ∃ ORF f, tž: ∀ x: x ∈ A ⇔ f(x) ∈ B
A ≤₁ B (množina A je 1-převoditelná na B) je-li f navíc prostá
množina A je m-úplná (resp. 1-úplná) pro třídu RSM pokud: je A RSM a ∀ jiná RSM je na ni m-převoditelná (resp. 1-převoditelná).
- 💡 budeme říkat pouze A je m-úplná nebo 1-úplná, dodatek „pro třídu RSM“ budeme vynechávat, protože jinými než RM a RSM se nebudeme zabývat.
- vlastnosti ≤1, ≤m
- $ A\leq_m B $ a $ B $ RM $ \Rightarrow A $ RM
- 💡 $ A\leq_m B $ a $ A $ není RM $ \Rightarrow B $ není RM (protože: $ (A\Rightarrow B)=(\neg B\Rightarrow \neg A) $)
- Dk: Je-li $ B $ RM a $ f $ je ORF převádějící $ A $ na $ B $, pak $ x ∈ A ⇔ f(x) ∈ B $ a tedy $ χ_A(x) = χ_B(f(x)) $. $ χ_A $ je jistě ORF a tedy $ A $ je RM.
- $ A\leq_m B $ a $ B $ RSM $ \Rightarrow A $ RSM
- 💡 $ A\leq_m B $ a $ A $ není RSM $ \Rightarrow B $ není RSM
- Dk: Je-li $ B $ RSM a platí-li $ B = dom φ_e $ a je-li $ f $ ORF, která převádí $ A $ na $ B $, pak $ A = dom λx[φe(f(x))] $ a jde tedy o RSM.
- $ \leq_m $ a $ \leq_1 $ (relace) jsou reflexivní a tranzitivní
- Dk: To, že jsou $ ≤_m $ a $ ≤_1 $ reflexivní relace plyne z toho, že identita je prostá ORF. Předpokládejme, že $ A ≤_1 B $ a $ B ≤_1 C $, nechť $ f $ je prostá ORF převádějící $ A $ na $ B $ a $ g $ buď prostá ORF převádějící $ B $ na $ C $. Pak $ h(x) = g(f(x)) $ je prostá ORF která převádí $ A $ na $ C $, což ukazuje, že $ ≤_1 $ je tranzitivní. Pro $ ≤_m $ platí týž argument s vynecháním prostoty.
- $ A $ $ m $-úplná & $ B $ RSM & $ A\leq_m B \Rightarrow B $ je $ m $-úplná
- 💡 platí pro 1-převoditelnost a 1-úplnost
- Dk: Toto plyne okamžitě z tranzitivity $ ≤_m $, $ ≤_1 $ a definice úplnosti.
- $ A\leq_mB \Rightarrow \overline A\leq_m\overline B $
- 💡 platí pro 1-převoditelnost a 1-úplnost
- Dk: Plyne přímo z definice převoditelnosti, převod $ A $ na $ B $ zajistí stejná funkce jako převod $ A $ na $ B $.
Problém zastavení K0 a jeho diagonála K[editovat | editovat zdroj]
- $ K_0 =\{\langle x, y\rangle_2\;|\;\varphi_x(y)\downarrow\}=\{\langle x, y\rangle_2\;|\;y\in W_x\} $ - problém zastavení
- $ K =\{x\;|\;\varphi_x(x)\downarrow\}=\{x\;|\;x\in W_x\} $ - diagonála $ K_0 $
💡 $ K_1 =\{x\;|\;W_x\neq\emptyset\} $
Věta ( $ K $, $ K_0 $ RSM $ \neg $RM ): $ K $ a $ K_0 $ jsou RSM, ale nejsou RM
| Dk (sporem jako u TS) |
|---|
: Z definice jsou obě RSM. Nechť $ φ_z $ označuje univerzální ČRF.
|
Věta ( 1-úplnost $ K $, $ K_0 $ ): Množiny $ K $ a $ K_0 $ jsou 1-úplné.
| Dk: |
|---|
: $ K $ je $ 1 $-úplná: $ K $ je RSM, stačí tedy ukázat, že libovolnou RSM lze na $ K $ převést prostou ORF.
|
Státnice -- Softwarové systémy
Složitost a vyčíslitelnost -- Tvorba algoritmů (10🎓), NP-úplnost (15🎓), Aproximační algoritmy (6🎓), Vyčíslitelné funkce a rekurzivní množiny (8🎓), Nerozhodnutelné problémy (9🎓), Věty o rekurzi (6🎓)
Datové struktury -- Stromy (32🎓), Hašování (13🎓), Třídění (10🎓)
Databázové systémy -- Formální základy: Relace (12🎓), Datalog (9🎓), Ostatní (0🎓) Modely a jazyky: SQL (7🎓), DIS (7🎓), Odborné (3) Implementace: Transakce (5🎓), Indexace (10🎓), Komprese (3)
Softwarové inženýrství -- Programovací jazyky a překladače, Objektově orientované a komponentové systémy, Analýza a návrh softwarových systémů
Systémové architektury -- Operační systémy, Distribuované systémy, Architektura počítačů a sítí
Počítačová grafika -- Geometrické modelování a výpočetní geometrie, Analýza a zpracování obrazu, počítačové vidění a robotika, 2D počítačová grafika, komprese obrazu a videa, Realistická syntéza obrazu, virtuální realita
🎓 - znamená kolikrát byla otázka u státnic