18. Jaderné záření

Sylabus

Jaderné záření: Interakce jaderného záření s prostředím a metody jeho detekce. Spektrometrie jaderného záření. Umělé zdroje jaderného záření

Státní závěrečná zkouška

Jaderné záření

Termín Jaderné záření nemusí mít nic společného s atomovým jádrem, jde totiž o tok mikroobjektů - elementárních částic, iontů, nebo i samotných atomových jader. Mikroobjekty procházející látkou interagují s jejími atomy (molekulami) třemi interakcemi (v závislosti na typu mikroobjektu):

• elektromagnetickou - kontakt nabitých částic s elektronovým obalem atomu
• silnou - srážky těžkých částic s jádry atomů dané látky
• slabou - mezi přítomnými leptony (resp. leptony a hadrony)

(samozřejmě i gravitační, ale ta je o dost menší než všechny ostatní a v jaderné fyzice se prakticky vždy zanedbává)

Interakce jaderného záření s prostředím

Rozlišíme několik případů interakce, dle typu mikroobjektů (částic nalétávajících na látku), proto nejprve zavedeme pojem: těžká částice je mikročástice, jejíž klidová hmotnost je srovnatelná nebo větší než klidová hmotnost protonu. Takovouto částicí může být atom, iont, jádro, libovolný baryon (natolik stabilní, že se dá o interakci s látkou vůbec uvažovat). Protože nabité částice lze snadno urychlit, v dalším se budeme zabývat pouze nabitými částicemi. Zástupcem nenabitých částic bude foton.

Těžké částice a látka

Vzhledem ke klidové hmotnosti mnohem větší, než je hmotnost elektronu, bude t.č. interagovat s jádry atomů látky - dojde ke srážkám a k rozptylu.

---

Odvození Rutherfordova vzorce pro rozptyl

Pro popis rozptylu definujeme diferenciální účinný průřez jako poměr celkového počtu částic dN, který se za jednotku času rozptýlí do prostorového úhlu z intervalu ($ \Omega,\Omega + d\Omega $), a počtem částic n, které projdou jednotkovou plochou za jednotku času:

$ d \sigma = \frac{dN}{n} $

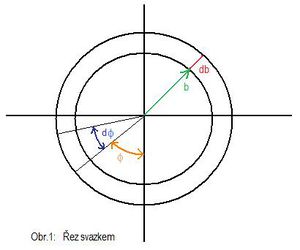
Hledáme závislost $ d\sigma $ na úhlu rozptylu, k tomu nám dopomůže srážkový parametr $ b = b(\theta) $, jenž udává vzdálenost asymptotické dráhy dopadající částice od osy, která prochází jádrem. Jsme v axiálních souřadnicích $ (b,\theta,\phi) $, kde $ \theta $ je úhel rozptylu.

Do intervalu ($ \theta, \theta + d\theta $) budou rozptýleny ty částice, které projdou ploškou $ 2 \pi b(\theta)db d\phi $, z těch do intervalu ($ \phi, \phi + d\phi $) projde $ b(\theta)db d\phi $. Počet částic dN je pak

$ dN = n b(\theta)db d\phi $

tedy vzorec pro diferenciální účinný průřez lze psát:

$ d \sigma = b(\theta)db d\phi = b(\theta)|\frac{db}{d \theta}|d \theta d\phi = \frac{b(\theta)}{sin(\theta)}|\frac{db}{d \theta}|d\Omega $

v posledním kroku jsem použila vztahu $ d\Omega = sin(\theta)d\theta d\phi $.

Tedy je vidět, že jakmile budeme mít b, dostaneme účinný průřez dle předchozího vztahu.

V Rutherfordově rozptylu se předpokládá, že rozhodující interakce je coulombické působení mezi jádrem a nalétávající částicí, a že hmotnost nalétávající částice je menší než jádra atomu látky, které je tak možné považovat za nehybné a vyšetřovat pohyb částice v centrálním poli jádra:

$ U(r) = \frac{\alpha}{r} $

v nekonečné vzdálenosti je celková energie dopadající částice s rychlostí $ v_{0} $ rovna kinetické $ E = \frac{1}{2}m v_{0}^2 $, moment hybnosti se zachovává $ L = mv_{0}b $, $ \alpha = \frac{Z_1Z_2e^2}{4 \pi \epsilon_{0} r} $

Rovnice pro celkovou energii částice je

$ E = \frac{m \dot r}{2} + \frac{\mathbf{L}}{2mr^{2}} + U(r) $ ???co raději ještě umocnit $ \dot r $ v prvním zlomku na druhou???

což tedy pro minimální vzdálenost částice s danou energií E od jádra $ r_{min} $ znamená:

$ E = \frac{\mathbf{L}}{2mr_{min}^{2}} + U(r_{min}) $

předpředchozí rovnice se dá integrovat - zjistit závislost r na čase

$ \frac{dr}{dt}=\left(\frac{2}{m}(E - U) - \frac{L^2}{m^2r^2}\right)^{\frac{1}{2}} $

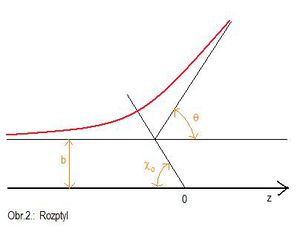
Pro získání srážkového parametru potřebujeme znát hodnotu úhlu $ \chi_{0} $ udávajícího místo nejmenší vzdálenosti mezi jádrem a částicí ($ r_{min} $):

Do předchozího dosadíme ze zachování momentu hybnosti $ L_{z}= L = mr^2 \dot \chi = konst $ substituci $ d\chi = \frac{L}{m r^2} dt $ a dostaneme vztah pro výpočet $ \chi_{0} $:

$ \chi_{0}= \int_{r_{min}}^{\infty}\frac{\frac{L}{r^2}}{(2m(E-U)- \frac{L}{r^2})^{\frac{1}{2}}}dr $

Dosadíme za $ r_{min} $ z rovnice pro celkovou energii částice a za L dosadíme $ L = mv_{0}b $ a po substituci a integraci dostaneme:

$ \chi_0 = arccos\left(\frac{\frac{\alpha}{mv_{0}^2b}}{(1+\left(\frac{\alpha}{mv_{0}^2b}\right)^2)^{\frac{1}{2}}} \right) $

z Obrázku2 dostaneme vztah mezi úhlem rozptylu a $ \chi_{0} $:

$ \theta = \pi - 2\chi_{0} $

takže konečně můžeme psát Rutherfordovu formuli pro rozptyl:

$ d\sigma = \frac{1}{4}\frac{\left(\frac{\alpha}{Z_1E}\right)^2}{sin^4(\frac{\theta}{2})} $ ???nechybí na pravé straně taky nějaký diferenciál???

cesta zpět do otázky č. 19. - Rozměr jádra

---

Při každé individuální srážce lze použít Rutherfordův vzorec, protože moment hybnosti v Hamiltoniánu tvoří bariéru, která částici znemožní se dostat k jádru tak blízko, aby se projevila kromě EM i silná interakce.

Částice po rozptýlení na jednom jádře pokračuje dál a dochází k mnohonásobnému rozptylu - odchylky trajektorie získané rozptylem na jádrech se skládají ale v průměru se anulují. Dá se ukázat (cituji Úlehla, SUK, Trka - Atomy, jádra, částice), že střední odchylka částic je přibližně nepřímo úměrná druhé mocnině kinetické energie částic.

Když energie těžké nabité částice těmito srážkami klesne na určitou hodnotu, vzroste pravděpodobnost nepružné srážky s atomy nebo molekulami látky, kde dojde k exitaci resp. ionizaci: daný atom, či molekula pak vyzáří foton resp. dojde k uvolnění elektronu, což je pro mikročástici velká energetická ztráta.

Ionizační ztráty připadající na element dráhy v intervalu energií $ E -mc^2 = E_k \in(1 MeV, 10^5 MeV) $ splňují přibližný vztah:

$ -\frac{dE_k}{dx}= \frac{z^2e^4n_e}{4\pi(\epsilon_0)^2m_e\beta^2c^2}\left[ln\left(\frac{2m_e\beta^2c^2}{I(1- \beta^2)}\right)-\beta^2\right] $

kde I je ionizační potenciál a $ n_e $ je koncentrace elektronů v prostředí, $ \beta = \frac{pc}{E} $

vztah lze psát když zavedeme $ v=\beta c $:

$ -\frac{dE_k}{dx}\approx z^2n_e f(v) = \tilde{f(E_k)} $

Zavedeme Lineární brzdící (ionizační) schopnost $ S=-\frac{dE_k}{dx} $ s významem ionizačních ztrát. Tato veličina s rostoucí kinetickou energií klesá ($ \approx \frac{1}{v^2} $), v oblasti velmi malých kinetických energií křivka nestoupá, protože částice nemají dostatečnou energii, potřebnou k ionizaci.

Při ionizaci může uvolněný elektron získat dost velkou energii, aby sám mohl ionizovat, takové elektrony lze registrovat.

Braggova křivka je závislost ionizační schopnosti částice na délce dráhy R, kterou v látce částice urazí.V dostatečně silné vrstvě látky se částice nakonec zastaví : dolet R je dráha, kterou částice proje do svého zastavení.

$ R = \int_{0}^R dx = \int_{E_k}^0 \frac{dE_k}{\tilde{f}(E_k)} $

pokud užijeme nerelativistické přiblížení $ \frac{dE_k}{dx} \approx mv\frac{dv}{dx} $ lze R psát v závislosti na rychlosti:

$ R = \frac{m}{z^2}\int\frac{vdv}{f(v)n_e} $

Závislost R na kinetické energii se popisuje empirickými vzorci specifickými pro dané energie, částice a prostředí.Náhodný charakter ionizace a mnohonásobný rozptyl způsobí, že částice stejného druhu se stejnou energií mají v daném prostředí různý dolet.

Elektron a látka

Elektrony interagují s atomy či molekulami látky především elektromagneticky. Při průchodu látkou ztrácejí elektony energii ionizačními ztrátami a brzdným zářením (Radiační ztráty).

V důsledku Principu nerozlišitelnosti platí pro ionizační ztráty energie elektronu v látce trochu jiný vztah než v případě těžkých nabitých částic:

$ -\left(\frac{dE_k}{dx}\right)_{ion}= \frac{z^2e^4n_e}{4\pi(\epsilon_0)^2m_e\beta^2c^2}\left[ln\left(\frac{2m_e\beta^2c^2}{I(1- \beta^2)}\right)+1-\beta^2-ln(2)(2(1-\beta^2)^{\frac{1}{2}}-1+\beta^2) + \frac{1}{8}(1-(1-\beta^2)^{\frac{1}{2}})^2 \right] $

Pozn: skaredy vzorcek, staci vediet, ze to zavisi na nabojoch, konstatne jemnej struktury $ \alpha $, hmote elektronu a na rychlosti elektronu ako 1/$ \beta^2 $, navyse sa mi zda, ze v tom vzorceku je mala chyba, pravdepodobne je z nejakej starsej ucebnice, takze sa ho neucte, navyse to urcite nebudu chciet na statniciach

Brzdné záření vzniká při interakci elektron-elektron nebo elektron-jádro. Radiační ztráty v důsledku brzdného záření jsou úměrné čtverci zrychlení (klasický pohled), proto jsou výraznější pro lehké částice.

$ -\left(\frac{dE_k}{dx}\right)_{rad}= nE_k \frac{Z^2r_{0}^2}{137}K(E) $

kde $ r_0 = \frac{e^2}{4\pi \epsilon_0 m c^2} $je klasický poloměr elektronu, n je počet atomů v objemové jednotce, K(E) závisí na energii tak, že pro $ E_k >> m_e c^2 $ je $ K(E) \approx 1 $

Tedy pro ztráty o stejné energii platí

$ \frac{\left(\frac{dE_k}{dx}\right)_{rad}}{\left(\frac{dE_k}{dx}\right)_{ion}} \approx E_k Z $

když uvážíme $ n_e \approx nZ $.

Takto můžeme definovat Kritickou energii jako energii, při které dochází k vyrovnání obou ztrát. Dále zavedeme Radiační délku $ X_0 $ vztahem:

$ E_k = E_{k0}exp(-\frac{x}{X_0}) $

$ X_0 $ je délka dráhy na které klesne energie elektronu na 1/e původní velikosti.

Elektron může v důsledku Brzdného záření ztratit velkou část své energie, proto není možné definovat dolet elektronu v látce stejně jako u t.n.č. Alternativní definice doletu elektronu jako maximální tloušťa látky, která elektron právě nepropustí.

Foton a látka

Přestože fotony nenesou náboj, z empirických poznatků víme, že tok fotonů procházejících látkou se zeslabuje s rostoucí tloušťkou této látky. Zákon zeslabení hustoty toku I svazku monoenergetických fotonů po překonání dráhy o délce x v daném prostředí:

$ I = I_0 exp(-\mu x) $

kde $ \mu $ je součinitel zeslabení.

Fotony jsou absorbovány v obalech atomů a jen z části opět vyzařovány se stejnou frekvencí, proto píšeme

$ \mu = n\sigma $

kde n je počet atomů v objemové jednotce, $ \sigma $ je účinný průřez udávající pravděpodobnost absorpce fotonu.

K zeslabení toku fotonů přispívají:

• Fotoefekt
• Comptonův rozptyl
• Tvorba párů elektron - pozitron

Celkový účinný průřez absorpce je součtem účinných průřezů pro tyto procesy:

$ \sigma = \sigma_f + \sigma_C + \sigma_p $

Fotoefekt

K fotoefektu dochází u elektronu vázaném v obalu atomu, energie fotonu je obvykle podstatně vyšší než vazbová energie $ U_{n} $. Účinný průřez $ \sigma_f $ bude mít maxima pro energie $ E_{\gamma} $ srovnatelné s vazbovými energiemi elektronu v jednotlivých slupkách $ U_{n} (n = K,L,M,...) $, bude klesat pro $ E_{\gamma} \in (U_n,U_{n+1}) $. Protože vazbové energie rostou s klesajícím n (energie potřebná k odtržení elektronu od atomu $ E_n = U_{n} $ s klesajícím n klesá) tak dochází k fotoefektu z 80 % ve slupce K. Fotoefekt se více projevuje u elektronů těžkých atomů, protože vazbová energie roste s rostoucím Z.

Účinný průřez fotoefektu na slupce K je:

$ \sigma_{f}^{K} =4 \sqrt{2} Z^5\sigma_0 \alpha^4 \left( \frac{m_e c^2}{h \omega}\right)^k $

kde k závisí na velikosti energie fotonu: pro $ E_{\gamma}>> U_{K} $ při $ h\omega << m_e c^2 $ je k = 7/2 a pro $ E_{\gamma}>> m_e c^2 $ je k = 1. $ \sigma_{0}=\frac{8\pi}{3}r_{0}^2 $ je účinný průřez Thompsonova rozptylu fotonu na elektronu,$ r_0 $ je klasický poloměr elektronu.

Celkový průřez fotoefektu klademe $ \sigma_{f}=\frac{5}{4}\sigma_{f}^{K} $.

Comptonův rozptyl

Když energie elektronů v obalu atomů látky je relativně malá ve srovnání s energií fotonu, nastává rozptyl fotonů na elektronech. Účinný průřez rozptylu na jednom elektronu:

$ \sigma_{C}^{e}= \frac{3}{4}\sigma_{0}\left( \frac{1+k}{k^2}\left[\frac{2(1+k)}{1+2k} - \frac{1}{k}ln(1+2k)\right] +\frac{1}{2k}ln(1+2k) - \frac{1+3k}{(1+2k)^2} \right) $

kde $ k=\frac{E_{\gamma} }{mc^2} $

Interakci fotonu z celým atomem pak dává celkový účinný průřez Comptonova rozptylu:

$ \sigma_{C}= Z \sigma_{C}^e $

Ten je tedy přímo úměrný atomovému číslu Z a nepřímo úměrný energii fotonu $ E_{\gamma} $.

Tvorba párů elektron - pozitron

Tento proces probíhá v poli atomového jádra nebo v poli elektronu, přičemž jejich přítomnost je nutná, aby byly splněny zákony zachování (Energie, hybnost). Pro vznik páru je nutné, aby energie nalétávajícího fotonu byla dost velká:

$ E_{\gamma} > 2mc^2 $ v poli jádra, nebo $ E_{\gamma} > 4mc^2 $ v poli elektronu.

Přibližný výraz pro účinný průřez tvorby párů v poli jádra o atomovém čísle Z je

$ \sigma_{p}^z= Z^2 \alpha r_{0}K(E_{\gamma},Z) $

kde pro K máme empirické vzorečky v závislosti na energii fotonu:

$ K = \frac{28}{9}ln\frac{2h\omega}{mc^2} - \frac{218}{27} $ platí pro $ E_{\gamma} >> mc^2 $

Celkový účinný průřez absorbce toku fotonů v látce se chavá přibližně jako

$ \sigma = \sigma_f +\sigma_C +\sigma_p \approx \frac{Z^5}{E_{\gamma}^{\frac{7}{2}}} + \frac{Z}{E_{\gamma}} + Z^2 ln(2E_{\gamma}) $

Detekce jaderného záření

Kromě informace o poloze mikročástice získáváme také její energii, hybnost a kvantová čísla.

Detektory částic rozlišujeme do tříd:

• Dráhové komory $ \times $ detektory, které registrují pouze počty částic
• Dle užívání destruktivních $ \times $ nedestruktivních metod měření (nemění se identita detekovaných částic)
• Dle předmětu detekce: nabitých $ \times $ neutrálních částic.

Detektor je charakterizován Detekční účinností (pravděpodobnost detekce), Mrtvou dobou (časový interval, kdy je detektor po registraci částice necitlivý), prostorovým, časovým a energetickým rozlišením.

Plynem plněné detektory

Při průchodu nabité částice plynem dochází k excitaci a ionizaci atomů či molekul plynu.

Mějme uzavřenou baňku s plynem (komoru), v ní zářič a obvod s kondenzátorem s proměnným napětím. Elektrické pole nutí ionty a elektrony k pohybu směrem k deskám kondenzátoru. V charakteristice obvodu jsou tři oblasti

• Platnosti Ohmova zákona (dochází k ionizaci, ale většina iontů a elektronů stihne zaniknout rekombinací)
• Nasyceného proudu (téměř všechny vytvořené ionty jdou k elektrodám)
• Ionizace nárazem (elektrony z primární ionizace získají tak velkou energii, že sami ionizují)

V 3. oblasti zavádíme Geigerův práh jako oblast, kde napětí už je dostatečně velké, aby jakkoli malá primární ionizace vzbudila velký růst proudu. Za Geigerovým prahem dochází k samostatnému výboji v plynu.

Ionizační komory pracují v oblasti nasyceného proudu. Měří tok částic procházející komorou. Kromě nabitých částic mohou detekovat i $ \gamma $ záření prostřednictvím elektronů uvolněných z obalu komory procesy jako je Comptonův jev, dále také neutrony při interakci s plynem, nebo pláštěm nádoby.

Proporcionální detektory pracují v oblasti ionizace nárazem, když primární ionizace je přímo úměrná velikosti ionizačního proudu. Tvoří je především skleněné válce, uvnitř pokovené (tvořící katodu) s tenkou anodou v ose válce, naplněné směsí argonu a metanu.Jejich mrtvá doba je $ 10^{-4} s $. Několik proporcionálních detektorů za sebou různě natočených může změřit několik bodů trajektorie částice, toto seskupení se nazývá Proporcionální komora.

Geigerovy - Mullerovy detektory pracují v oblasti Geigerova prahu. Oproti Proporcionálním detektorům je napětí na anodě tak velké, že nastává samostatný výboj a je nutné ho pro další detekci přerušit. Jedním ze způsobu přerušení výboje je přítomnost organického plynu, který pohlcuje UV záření vzniklé při rekombinaci, a tak snižuje pravděpodobnost fotoefektu z UV záření, tedy vznik dalších ionizace schopných elektronů. Při každém přerušení výboje se část molekul organického plynu rozštěpí, proto má G-M detektor omezenou životnost.

Scintilační detektory

Scintilace jsou záblesky, vzbuzené dopadajícími částicemi, scintilátor je látka, která po excitaci nabitými částicemi vysílá EM záření (viditelné + UV), příklady scintilátorů: anorganické nebo organické krystaly, kapalné, plastické a skleněné látky, vzácné plyny.

Každý scintilační detektor se skládá ze tří částí:

• scintilátoru
• světlovodu
• fotonásobiče

Světlovod vede světelný signál ze scintilátoru do fotonásobiče, který mění slabé světelné signály na elektrické pulsy na principu fotoefektu. Z fotokatody je vyslán přibližně jeden elektron na 20 absorbovaných fotonů.

Polovodičové detektory

Nabitá částice uvolňuje nositele náboje tentokrát v pevné látce. Požadované vlastnosti detektoru s pevnou látkou:

• Energie spotřebovaná na vytvoření páru nositelů náboje je malá ($ 3 eV $)
• Míra rekombinace a záchytu nositelů náboje je malá
• Pohyblivost nositelů náboje je velká a stejná pro obě znaménka
• Měrný odpor látky je velký, tedy fluktuace proudu v látce (šum) jsou malé

Nejlépe použitelnou látkou pro detekci jsou polovodiče, protože splňují první tři body a 4. kompenzují vlastností p-n přechodu - v polovodiči p jsou nositely náboje kladné díry a v n zas elektrony, na hranici p-n přechodu je oblast bez volných nábojů, která se zvětší při vložení napětí, a tato oblast je citlivý objem detektoru, kde detekovaná nabitá částice vytváří ionty, které jsou odvedeny na elektrody. Měří se změna náboje na elektrodách.

Navíc mají polovodičové detektory dobré rozlišení, krátkou mrtvou dobu a velkou detekční účinnost u záření $ \gamma $.

Používá se několik typů polovodičových detektorů:

Křemíkový s p-n přechodem, Křemíkový s příměsí lithia s p-i-n přechodem - příměs umožňuje zvětšení citlivé oblasti, Germaniový p-i-n,.

Čerenkovův detektor

V Radiátoru (Blok z opticky průzračné látky s velkým indexem lomu) se vytvoří Čerenkovovo záření (cz wiki o čer.záření), které registruje fotonásobič. Používá se především v subjaderné fyzice.

Kalorimetry

Měří energii všech částic vyslaných v intervalu prostorového úhlu. Jde o detektor destruktivní, protože se využívá interakce částic s prostředím za vzniku jiných částic. Kalorimetry se skládají z absorbátorů a detektorů.

Elektromagnetický kalorimetr měří energii fotonů a elektronů pomocí EM interakce. Energetické rozlišení je nepřímo úměrné odmocnině z energie částice.

Hadronový kalorimetr měří energii hadronů a neutronů pomocí silné interakce s atomovými jádry.Energetické rozlišení je také nepřímo úměrné odmocnině z energie částice.

Pro měření energie neutrin se využívá slabé interakce neutrin s atomovými jádry.

Dráhové komory

Nabitá částice při svém letu ionizuje prostředí, proto se v náplni komory vytvoří stopa dráhy částice.

Jaderné foto-emulze jsou velmi citlivé fotografické emulze (bromid stříbrný), které se ozařují částicemi. Po vyvolání se prohlížejí mikroskopem.

Mlžné komory jsou komory naplněné přesycenou párou, která kondenzuje na iontech vytvořených nabitou částicí. Přesycení par se dosahuje adiabatickou expanzí (Wilsonovy komory), nebo difuzí par s velkým teplotním gradientem. Mlžné komory se umísťovaly do magnetického pole, kde bylo možné dle zakřivení dráhy částice měřit náboj a hybnost částice. Dnes se již nepoužívají.

Bublinové komory - uzavřené nádoby naplněné přehřátou kapalinou (kapalina s teplotou nad bodem varu, vzniká expanzí) v okolí iontů začne kapalina vřít - vytvoří se bublinky. Bublinové komory se taktéž umisťují do magnetického pole a fotí se z různých směrů. Lze pak stanovit druh, znaménko náboje a hybnost částice.

Jiskrové komory - mezi dvěma elektrodami s vysokým napětím nastane výboj způsobený ionizací plynu (jiskra). Používají se při detekci částic s vysokými energiemi.

Spektrometrie jaderného záření

Spektrometrie nebo Spektroskopie ze zabývá měřením závislosti energie na vlnové délce/frekvenci obecného záření.

Spektrometrie nabitých částic

Z doletu těžké nabité částice R (viz oddíl Těžké částice a látka) lze poměrně přesně určit její energii. Dolet lze přímo měřit dráhovými detektory. Většina těžkých částic má poměrně krátký dolet, proto se jejich energie měří jinak:

V ionizační komoře se měří celkový signál vytvořený částicí do jejího zastavení. Ve scintilačních a polovodičových detektorech - velikost náboje na anodě fotonásobiče je úměrná energii, kterou částice ztratí při průletu detektorem. Pro měření energie částice je tedy nutné, aby se částice v detektoru zastavila.

Magnetické spektrometry

V nerelativistickém a nekvantovém případě je energie nabité částice v magnetickém poli dána:

$ H= \frac{1}{2m}(\mathbf{p}-Ze\mathbf{A})^2 = E $

Pokud bude magnetické pole homogenní $ \mathbf{B}= (0,0,B), \mathbf{A} = (-\frac{B}{2}y,\frac{B}{2}x,0) $ vztah pro energii bude:

$ H= \frac{1}{2m}\left(p^2 - ZeBL_z + \frac{Z^2 e^4 B^2}{4}(x^2 +y^2) \right) =E $

kde $ L_z = xp_y-yp_x $ je z-ová složka momentu hybnosti.

Z Hamiltonových rovnic dostaneme

$ \ddot x; = \omega \dot y ; \ddot y = \omega \dot x ; p_z = konst. $

kde $ \omega = \frac{ZeB}{m} $ je Larmorova frekvence.

Průmět trajektorie částice do roviny (x,y) je kružnice, $ r^2 = konst. $, proto $ v^2 = \omega^2 r^2 = konst'. $

V případě, že $ p_z=0 $, bude energie částice v okamžiku vstupu do magnetického pole

$ E= \frac{p_{x}^2 + p_{y}^2}{2m}= \frac{1}{2}m \omega^2 r^2 = \frac{1}{2m} Z^2 e^2 B^2 r^2 $

Tedy energii částice získáme, budeme-li znát B,m,r,Z.

částice se stejnou energií budou mít v homogenním magnetickém poli stejné r, tedy dopadnou zhruba do stejných míst.

Spektrometrie záření $ \gamma $

Pod pojmem spektrometrie EM záření se většinou myslí měření spektra, tj. závislosti energie na vlnové délce záření (zde je totiž trochu přijatelnější uvažovat o vlnové délce, než u těžkých nabitých částic).

Pro fotony $ \gamma $ s malou energií ($ \approx 0,1 MeV $) a tedy relativně velkou vlnovou délkou ($ \lambda \approx 10^{-12} m $) lze měřit jejich spektrum pomocí difrakce na krystalové mřížce. Energii $ \gamma $ záření pro velké energie fotonů ($ \geq 0.1 MeV $) měříme prostřednictvím interakce s prostředím, kde vznikají nabité částice, které lze snadněji detekovat.

Energii záření $ \gamma $ lze získat měřením součinitele zeslabení v důsledku interakce s látkou, který závisí na energii $ \mu = n\sigma(E_k) $:

Ať $ n(x) $ je počet registrovaných $ \gamma $ fotonů po průchodu absorbátorem o tloušťce x, počet nalétávajících fotonů je n(0), potom je součinitel zeslabení definován jako

$ \frac{n(x)}{n(0)} = exp(-\mu x) $

po zlogaritmování ho můžeme získat jako směrnici přímky

$ -\mu x = ln (n(x))- ln (n(0)) $

Závislost $ \mu(E_k) $ je známa pro konkrétní materiály s dobrou přesností.

Nejčastěji se pro měření energie $ \gamma $ záření používají scintilační nebo polovodičové detektory. Při absorpci monoenergetického záření $ \gamma $ se získá spektrum amplitud pulsů charakteristického tvaru, jednotlivé části odpovídají různým procesům, které proběhly při interakci $ \gamma $ fotonu s prostředím (Fotoefekt, Comptonův rozptyl, tvorba párů elektron - pozitron).

Spojité spektrum, které vytvářejí signály vyvolané comptonovskými elektrony, je ukončeno Comptonovou hranou - případ rozptylu $ \gamma $ fotonu na úhel 180°.

Čárové spektrum - sekundární maxima vznikají, když jeden nebo oba fotony pocházející z anihilace uniknou z detektoru.

Umělé zdroje jaderného záření

Pomocí urychlených stabilních nabitých částic lze získat mnoho typů jaderného záření:

• proud urychlených elektronů, protonů nebo iontů
• ve vhodném uspořádání může proud elektronů vybudit svazky fotonů
• po dopadu urychlených protonů lze získat svazky mezonů, mionů a neutrin
• ve vhodných terčících lze vybudit svazek neutronů

Urychlovače pracují jako zdroje jaderného záření pro energie od 1 MeV do 1 TeV.

Rozlišujeme je do tříd dle:

• tvaru trajektorie - lineární či kruhové
• režimu - spojitě pracující či pulsní
• působení - urychlení v jednom procesu či mnohonásobné působení

Charakterizujeme je Maximální dosažitelnou energií, hustotou toku částic ve svazku, intenzitou elektrického proudu.

Principy urychlování

Elektrické pole dodává částici energii

$ \frac{dE}{dt}=Ze\mathbf{v}\epsilon $

kde $ \epsilon $ je vektor intenzity elektrického pole

Pohybuje-li se nabitá částice rychlostí kolmou ke směru magnetické indukce homogenního magnetického pole, její trajektorie je kružnice s poloměrem

$ r = \frac{p}{ZeB}= \frac{m_0 v}{ZeB} $

kde $ m_0 $ je klidová hmotnost částice.

Pak Cyklotronová frekvence je dána

$ \omega_C=\frac{v}{r}=\frac{ZeB}{m_0}=\frac{ZeBc^2}{E} $

Typy urychlovačů

Kruhové

• Betatron - indukční urychlovač elektronů

Elektrony se pohybují v evakuovaném prstenci urychlovány elektrickým napětím, vytvořeným elektromagnetickou indukcí (časově proměnné magnetické pole), musí být splněna Betatrononová podmínka: Poloměr rovnovážné dráhy je během urychlování konstantní.

• Cyklotron - rezonanční kruhový urychlovač protonů a těžších iontů

Uvnitř vakuové komory jsou dvě elektrody, uprostřed urychlovače je zdroj iontů, které se pak pohybují po spirále s rostoucím poloměrem, létají skrz urychlovací štěrbinu mezi elektrodami.

• Synchrotron

Elektrony běhají po kružnici s konstantním poloměrem při konstantní frekvenci urychlujícího napětí s rostoucí magnetickou indukcí. V počáteční fázi pracují jako Betatron, pak dochází ke změně režimu práce na pulsní.

• Vstřícné svazky

V experimentech se srážkami částic je třeba dosáhnou co největší relativní energie srážejících se částic, což se může realizovat tak, že jedna částice "stojí" a druhá do ní narazí, ale efektivnější je urychlit obě částice a poslat je proti sobě.

Lineární

• Elektrostatické

Skládají se z urychlovací trubice a zdroje vysokého napětí, užívalo se Van de Graaffova generátoru. Tandemový urychlovač používá několik takových generátorů, umožní tak po sobě jdoucí urychlení.

• Vysokofrekvenční

Urychlovací trubice obsahuje několik různě dlouhých válcových elektrod (jejich délka roste se vzdáleností), které jsou připojeny ke zdroji vysokofrekvenčního napětí. Nastavení frekvence je takové, aby při průchodu štěrbinou mezi elektrodami částice procházela vhodným urychlujícím napětím.

Státní závěrečná zkouška