Protiseminár - Lieove algebry a exponenciála
Lieove algebry a exponenciála
Ako sa pracuje s maticami rotácií a čo to je generátor rotácie?
Ako to súvisí s momentom hybnosti? Chcete vedieť, ako exponenciálou posunúť alebo otočiť vektor?
Čo je to exponenciála komplexného čísla?
A ako komplexifikácia $ \mathbf R^3 $ zafixuje bázové vektory a rozdelí priestor na tri časti?
Alebo by ste chceli vedieť poriadne vyriešiť diferenciálnu rovnicu bez hádania riešenia?
A čo je to Campbell-Baker-Hausdorfova veta?
Príďte sa pozrieť!
aká silná je matematika v rukách fyzika:)
Kedy a kde?
V pondelok 5.1.2009 o 18:00 v T2
Čo so sebou?
Hrnček na čaj, tentoraz ten čaj určite bude, beriem konvicu:)
♦♦♦
Plán seminára:
Grupa -> algebra
- 2D rotácie, vlastnosti grupy, ortogonálne matice ako grupa, infinitezimálna rotácia.
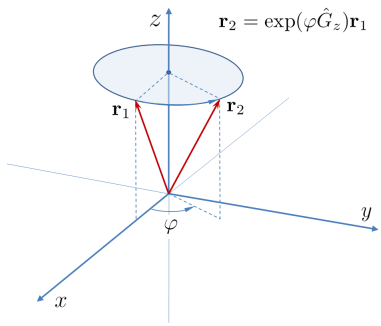
- 3D rotácie, infinitezimálne rotácie, generátory, skladanie.
- Komutátor rotácií: $ \mathbf {R}_x \mathbf{R}_y \mathbf {R}_x^{-1}\mathbf{R}_y^{-1} $ vs. $ [\mathbf A_x, \mathbf A_y] \approx \mathbf A_z $
Algebra -> grupa
- Diferenciálna rovnica
$ \frac{df}{dx} = kf $,
fyzikálne príklady a jej špeciálny prípad $ \frac{df}{dx} = f $. Vytvorenie exponenciály z Eulerovej metódy.
- Čo je to exponenciála komplexného čísla? Eulerov vzorec.
- Konečné rotácie ako exponenciála generátora, exponenciála operátora. Význam v kvantovej mechanike (generátor posunutia - hybnosť, otočenia - moment hybnosti).
- Campbell-Baker-Hausdorfova veta s jedným komutátorom: ak $ \hat A $ aj $ \hat B $ komutujú s $ [\hat A, \hat B] $, tak $ e^{\hat A+ \hat B} = e^{\hat A} e^{\hat B} e^{-\frac{1}{2}[\hat A,\hat B]} $.
Lineárne reprezentácie
- grupa a jej reprezentácia (reprezentácia grupy lineárnymi operátormi)
- invariantné podpriestory a blokové matice
- rozklad reprezentácie na ireducibilné
- skladanie reprezentácií