Úvod do strojového učení (v počítačové lingvistice)

{{predmet|Úvod do strojového učení (v počítačové lingvistice)|Barbora Vidová-Hladká]],
Pavel Schlesinger,
[[Kiril Ribarov|PFL054}}

Tohle jsou ne nutně úplné poznámky ze ZS 2008/9 -- Tuetschek 18:59, 23 Jan 2009 (CET)

Stránka předmětu, obsahuje slajdy
R-tahák ze zápisků ze cvičení, měl by obsahovat většinu důležitých funkcí
Literatura: Tom Mitchell (1997): Machine Learning. McGraw/Hill, ISBN 0-07-042807-7.

Úvod

Učení v našem smyslu je získávání zkušeností, učení se novým poznatkům. Stroj je počítač, který umí jenom počítat. Formálně:

Počítač se učí řešit úlohu třídy $$ T $$ se zkušeností $$ E $$ a úspěšností měřenou kritériem $$ P $$ , jestliže se jeho úspěšnost zkušeností zvyšuje.

Např.: $$ T $$ = parsing, $$ E $$ = treebank, $$ P $$ počet správně určených hran.

Zkušenost je přímá (přímo uvést, které postupy jsou povolené a které ne) a nepřímá (udává "dobré" postupy na základě trénovacích dat). Získávání zkušenosti může být řízené (s učitelem, kdy $$ E $$ = trénovací data), semi-supervised (kdy systém generuje postupy a něco je známkuje) nebo neřízené. Trénovací data by měla být vybraná s ohledem na testovací data.

Pro řízené strojové učení máme trénovací data: $X = x_1, x_2, \dots x_n$ s výstupními hodnotami $$ Y $$ a hledáme cílovou funkci $c:X\to Y, c(x_i) = y_i$ . Hledáme ji nad prostorem hypotéz (modelem) $$ H $$ ; tj. hledáme $h\in H: h(x_i) = c(x_i)\ \forall i\in 1,\dots n$ .

Několik konceptů

Tato část je neúplná a potřebuje rozšířit. doplnit, vysvětlit místa označená "(?)"

Postup učení jako vyhledávání: Máme množinu možných hypotéz, v ní podmnožinu hypotéz konzistentních s trénovacími daty a v této podmnožině se někde nachází optimální hypotéza. Pomocí stroj. učení se jí přibližujeme, od startovací hypotézy se postupně dostaneme do něčeho, co je konzistentní s trénovacími daty, ale ne nutně k optimu.

Vstupní hodnoty $$ X $$ prostoru hypotéz jsou buď reálné, diskrétní, nebo kategoriální. Výstupní hodnoty taktéž, potom je pro reálné hodnoty strojové učení regresí, kdežto pro kategoriální klasifikací.

Trénování je možné:

dávkově (všechna trénovací data najednou)
inkrementálně (dostávám instance jednu po druhé, mám náhodný výběr s návratem, postupně bez návratu (?))
online (dostávám trénovací instance jednu po druhé, až když jsou k dispozici)

Bias je nějaký apriorní předpoklad. Může být dvojitého typu:

absolutní -- např. "hledaná hypotéza je prvkem prohledávané množiny" (?)
preferenční -- preferují se hypotézy vyhovující nějakému kritériu (např. Occamově břitvě)

Se šumem v datech se musí počítat, vzniká kvůli chybě měření nebo chybě modelu. Data musí ale být konzistentní (?).

Occamova břitva je kritérium jednoduchosti: vybrat nejjednodušší hypotézu, která pasuje na trénovací data (nabízí-li se víc možností).

Testování hypotéz -- úspěšnost hypotézy na trénovacích datech je odhadem její úspěšnosti na testovacích datech (+ intervaly spolehlivosti (?)). Problém je přetrénování: při příliš velkém množství trénovacích dat klesá chyba na trénovacích, ale roste chyba na testovacích datech. K zjištění očekávané úspěšnosti na testovacích datech se může používat i křížová validace: rozdělím trénovací data na podmnožiny a potom vždycky natrénuju na jedné podmnožině a testuju úspěšnost na zbytku dat; nakonec spočítám průměrnou chybu.

Teoretické aspekty:

Lze určit hranice pro velikost prostoru hypotéz, přesnost aproximace, pravděpodobnost vydání úspěšné hypotézy a nutnou velikost trénování?
Kolik trénovacích příkladů je třeba, aby učení s vysokou pravděpodobností konvergovalo k úspěšné hypotéze?
Jaká je výpočetní složitost učení, které je úspěšné?
Kolik případů bude klasifikováno špatně, než systém dojde ke správné hypotéze?
Naučitelnost: Požadujeme, aby se systém s velkou pravděpodobností naučil hypotézu, která je přibližně správná.

Testování úspěšnosti algoritmů

Máme několik měr, které se všechny vztahují k tabulce confusion matrix.

Tabulka pro posuzování úspěšnosti algoritmů (confusion matrix)
Testovací data	Reálná hodnota: 1	Reálná hodnota: 0
Klasifikace: 1	tp	fp
Klasifikace: 0	fn	tn

Accuracy je čistě poměr správně klasifikovaných a všech testovacích instancí, tj. $A = \frac{tp + tn}{tp + fp + tn + fn}$
Precision: $P = \frac{tp}{tp + fp}$ a recall: $R = \frac{tp}{tp + fn}$ se vždycky uvádějí dohromady.
F-measure: $F = \frac{2PR}{P+R}$ je kombinací předchozích dvou, většinou odráží chování algoritmu nejlépe.

Uspořádání hypotéz

Cílem tohoto typu učení je vytvoření boolovské funkce z množiny trénovacích příkladů. Hypotézu tu reprezentujeme jako $$ n $$ -tici "povolených" hodnot proměnných z trénovacích příkladů, přičemž pro hypotézu může být hodnotou:

Specifická hodnota dané proměnné (tj. povolená je jedna hodnota)
"?" (tj. na hodnotě této proměnné nezáleží, povolené je všechno)
" $\emptyset$ " (tj. nevyhovuje žádná hodnota této proměnné)

Pokud instance $$ x $$ vyhovuje všemi svými hodnotami proměnných povoleným hodnotám pro hypotézu $$ h $$ , potom $$ h(x) = 1 $$ , tj. hypotéza $$ h $$ klasifikuje $$ x $$ jako pozitivní příklad.

Potom nejobecnější hypotéza je taková, která cokoliv klasifikuje jako pozitivní případ, tj. $(?, ?, ?, \dots, ?)$ a nejspecifičtější hypotéza taková, která vše klasifikuje jako negativní, tj. $(\emptyset, \emptyset,\dots,\emptyset)$ .

Máme dán popis instancí $$ X $$ , tj. možné hodnoty proměnných, potom prostor všech možných hypotéz $$ H $$ , cílovou funkci $c: X\to \{0,1\}$ a trénovací data (pozitivní i negativní příklady $D = (<x_1, c(x_1)>, <x_2, c(x_2)>,\dots)$ . Hledáme takovou hypotézu, která by odpovídala cílové funkci na všech trénovacích příkladech: $h\in H: \forall x\in X: h(x) = c(x)$ . Hypotéza, která je "vhodně dobrou" aproximací cílové funkce nad trénovacími daty, bude i "vhodně dobrou" aproximací nad ostatními daty.

Definice

Pro prohledávání hypotéz máme vodítko: uspořádání podle specifičnosti.

Řekneme, že příklad $x\in X$ vyhovuje hypotéze $h\in H$ , právě když $$ h(x) = 1 $$ .
Hypotéza $h\in H$ je obecnější než hypotéza $j \in H$ ( $h \geq_{g} j$ ), právě když $\forall x\in X: j(x) = 1\Rightarrow h(x) = 1$ (můžeme říct, že $$ j $$ je specifičtější než $$ h $$ ).
Hypotéza $h\in H$ je striktně obecnější než $j \in H$ ( $h >_{g} j$ ), pokud $$ h $$ je obecnější než $$ j $$ , ale $$ j $$ není obecnější než $$ h $$ .
Relace $\geq_{g}$ je částečné uspořádání nad prostorem $$ H $$ .

Další definice:

Hypotéza $$ h $$ pokrývá pozitivní příklad $x\in X$ , právě když ho správně klasifikuje jako pozitivní.
Hypotéza $$ h $$ je konzistentní s trénovacími daty $$ D $$ , právě když $h(x) = c(x)\ \forall <x,c(x)>\in D$ .
Prostor možností (version space) $VS_{H,D}$ vzhledem k prostoru hypotéz $$ H $$ je podmnožina hypotéz konzistentních s trénovacími daty $$ D $$ .
Hranice obecnosti (general boundary) $$ G $$ vzhledem k $$ H $$ a $$ D $$ je množina nejobecnějších hypotéz z $$ H $$ konzistentních s $$ D $$ . Proti tomu Hranice specifičnosti (specific boundary) $$ S $$ vzhledem k $$ H $$ a $$ D $$ je množina nejspecifičtějších hypotéz z $$ H $$ konzistentních s $$ D $$ .

Algoritmus Find-S

Nalezne nejspecifičtější hypotézu, která ještě vyhovuje trénovacím datům.

Vezmi nejspecifičtější hypotézu $h\in H$
$\forall x$ pozitivní trénovací příklad a $\forall a_i$ atribut reprezentace $$ h $$ : pokud hodnota $$ a_i $$ u $$ x $$ neodpovídá $$ h $$ , nahraď hodnotu $$ a_i $$ v $$ h $$ nejbližší obecnou hodnotou, která odpovídá $$ x $$
Po projití všech pozitivních příkladů vrať upravené $$ h $$

Find-S vrátí nejspecifičtější hypotézu konzistentní s pozitivními trénovacími příklady. Za předpokladů, že prohledávaný soubor hypotéz obsahuje cílovou funkci $$ c $$ a trénovací data neobsahují chyby, bude nalezená hypotéza konzistentní i s negativními trénovacími příklady, tj. s celými trénovacími daty.

Je-li víc správných hypotéz, nalezneme takto jen jednu z nich, navíc neodhalíme nekonzistenci trénovacích dat. Nemusí existovat ani jen jedna nejspecifičtější hypotéza. Problém nalezení všech konzistentních hypotéz řeší algoritmus Candidate-Elimination.

Algoritmus Candidate-Elimination

Tato část je neúplná a potřebuje rozšířit. dovysvětlit "(?)"

Algoritmus pracuje s prostorem možností, určeným hranicí obecnosti a hranicí specifičnosti. To je možné proto, že platí následující věta:

Věta o reprezentaci prostoru možností: $VS_{H,D} = \{h\in H: \exists s\in S, \exists g\in G: (g\geq_g h\geq_g s)\}$ .

Postup algoritmu:

Do $$ G, S $$ přiřaď množinu nejobecnějších, resp. nejspecifičtějších hypotéz z $$ H $$
Postupuj přes trénovací příklady $d\in D$ :
Je-li příklad $ d\in D $ pozitivní:
1. Odstraň z $$ G $$ hypotézy nekonzistentní s $$ d $$ .
2. Každou s $$ d $$ nekonzistentní hypotézu z $$ S $$ odstraň a přidej do $$ S $$ její minimální zobecnění konzistentní s $$ d $$ , pro které existuje nějaká obecnější hypotéza v $$ G $$ . Odstraň pak z $$ S $$ hypotézy, které jsou obecnější než jiné hypotézy v $$ S $$ .
Je-li příklad $ d\in D $ negativní:
1. Odstraň z $$ S $$ hypotézy nekonzistentní s $$ d $$ .
2. Každou s $$ d $$ nekonzistentní hypotézu z $$ G $$ odstraň a přidej do $$ G $$ její minimální specializaci konzistentní s $$ d $$ , pro kterou existuje nějaká specifičtější hypotéza v $$ S $$ . Odstraň pak z $$ G $$ hypotézy, které jsou specifičtější než jiné hypotézy v $$ G $$ .
Na konci vrať $$ G, S $$ jako reprezentaci prostoru možností.

Pokud chci uznávat dvě "povolené" hodnoty pro jeden atribut a ne jen jednu nebo všechny, můžu si zvětšit prostor hypotéz na množinu všech podmnožin množiny instancí $$ X $$ . Potom můžeme použít CE algoritmus, ale systém není schopen klasifikovat instance "za hranicí" trénovacích dat (?).

Induktivní předpoklad

Tato část je neúplná a potřebuje rozšířit. dovysvětlit "(?)"

Abychom zachytili strategii, podle které systém generalizuje za hranici trénovacích dat při klasifikaci nových instancí, definujeme induktivní předpoklad:

$(D_c\wedge x_i)\vdash L(x_i, D_c)$ , tj. klasifikace instance $$ x_i $$ algoritmem $$ L $$ natrénovaným na $$ D_c $$ je induktivně odvoditelná z oné instance a trénovacích dat.
Induktivní předpoklad (inductive bias) algoritmu $$ L $$ je minimální množina tvrzení $$ B $$ taková, že pro libovolnou cílovou funkci $$ c $$ definovanou nad instancemi $$ X $$ a odp. trénovací data $$ D_c $$ platí: $\forall x_i \in X: (B\wedge D_c\wedge x_i)\vdash L(x_i, D_c)$ , tj. klasifikace $$ x_i $$ algoritmem $$ L $$ natrénovaným na $$ D_c $$ je dokazatelná z instance, trénovacích dat a induktivního předpokladu.

Induktivní předpoklad algoritmu CE je $B = \{c\in H\}$ , tj. "cílová funkce je obsažena v prostoru hypotéz". Potom totiž platí i $c\in VS_{H,D}$ a $\forall h\in VS_{H,D}: h(x_i) = L(x_i,D_c)$ , tj. i $$ c(x_i)=L(x_i, D_c) $$ .

Např. algoritmus ROTE-LEARNER, který jen skladuje v paměti trénovací příklady a pak vydává výsledek jen tehdy, je-li reálný příklad ekvivalentní nektrému z nich, má prázdný induktivní předpoklad.

Proti tomu Find-S předpokládá $c \in H$ a navíc, že všechny příklady jsou negativní, pokud jejich protějšek nepřináší novou znalost (?). Induktivní učící systém, který používá CE a prostor hypotéz $$ H $$ , je ekvivalentní deduktivnímu učícímu systému, který používá dokazování logických vět a induktivní předpoklad " $$ H $$ obsahuje cílovou funkci".

Perceptron

Tato část je neúplná a potřebuje rozšířit. Doplnit, opravit (nevím, jestli to chápu ;))

Mějme nějaké trénovací příklady $(x_i,y_i)\ i=1\dots n$ , funkci $\mathbf{GEN}(x)$ , která pro vstup $$ x $$ vygeneruje všechny možné výstupy, reprezentaci $\Phi: (x,y)\to\mathbb{R}^d$ (mapuje dvojice $$ (x,y) $$ na vektor nějakých atributů) a vektor parametrů $\overline{\alpha}\in\mathbb{R}^d$ .

Např. máme trénovací příklady jako věty a jim odpovídající sekvence tagů, funkce $\mathbf{GEN}(x)$ generuje všechny možné sekvence tagů příslušné délky a $\Phi$ jsou atributy indikující určité vlastnosti, definované jako suma lokálních vlastností (závisejících na nějakém slově a jeho tagu, předchozích dvou tagách a pozici ve větě; např. booleovská indikace toho, že slovo je the a tag ukazuje DET, tj. člen).

Pro klasifikaci nových instancí použijeme funkci $F(x) = \mathrm{argmax}_{y\in\mathbf{GEN}(x)} \Phi(x,y)\cdot\overline{\alpha}$ . Úkolem učení je tady zjistit správné hodnoty $\overline{\alpha}$ , aby klasifikace pomocí $$ F(x) $$ byla co nejpřesnější. Algoritmus učení vypadá následovně:

Nastavit $\overline{\alpha} = 0$
Pro (předem systémem pokus-omyl určený) počet kroků $ T $ a pro všechna $ i = 1,\dots,n $:
1. Spočíst $z_i = \mathrm{argmax}_{z\in\mathbf{GEN}(x_i)}\Phi(x_i,z)\cdot\overline{\alpha}$ .
2. Pokud $(z_i\neq y_i)$ , potom upravit $\overline{\alpha} = \overline{\alpha} + \Phi(x_i,y_i) - \Phi(x_i,z_i)$ .
Vrátit parametry $\overline{\alpha}$ .

Konvergence

Tato část je neúplná a potřebuje rozšířit. dopsat text

Dá se dokázat, že algoritmus se opravdu naučí to, co má (konverguje ke správnému výsledku) a taky že na neznámých datech bude zaručeně pracovat nějak dobře.

$\overline{\mathbf{GEN}}$ -- špatné klasifikace
Separovatelnost trénovací sekvence s marginem $\delta$ : $\exists\mathbf{U}, ||\mathbf{U}||=1$ takové, že $\forall i, \forall z\in\overline{\mathbf{GEN}}(x_i): \mathbf{U}\cdot\Phi(x_i,y_i) - \mathbf{U}\cdot\Phi(x_i,z)>\delta$
Pro separovatelné počet chyb po konečném počtu kroků algoritmu je $\leq \frac{R^2}{\delta^2}$ , kde $\forall i, \forall z\in\overline{\mathbf{GEN}}(x_i): ||\Phi(x_i,y_i) - \Phi(x_i,z)||\leq R$ .
Pro neseparovatelné -- $D_{U,\delta}$ : jak daleko je od separování, počet chyb $\leq\min_{U,\delta}\frac{(R+D_{U,\delta})^2}{\delta^2}$

Volený perceptron

Tato část je neúplná a potřebuje rozšířit. dopsat text, formalizaci

Vylepšení (voted perceptron): pamatujeme si $\overline{\alpha}_i$ ze všech kroků algoritmu a když dostaneme novou instanci, počítáme její klasifikace postupně za pomoci všech $\overline{\alpha}_i$ a jako výslednou klasifikaci vrátíme tu, která se vyskytuje nejčastěji.

Pravděpodobnost, že se sekne na netrénovacích datech, je $\frac{2}{n+1}E_{n+1}\left[\min_{U,\delta}\frac{(R+D_{U,\delta})^2}{\delta^2}\right]$

Rozhodovací stromy

Jsou induktivní algoritmy, vytvořené ke klasifikaci instancí, které popisují pomocí "disjunkce konjunkcí". Můžeme je použít, když instance jsou popsány atributy a hodnotami a cílová funkce je diskrétní. V trénovacích datech můžou být i chyby nebo nevyplněné atributy, není to až tak citlivé.

Cílová funkce je tu reprezentována právě rozhodovacím stromem (sekvencí rozhodnutí if-then-else), klasifikace se pak provádí průchodem stromem od kořene k listům, kdy se testuje hodnota jednoho atributu instance pro každý uzel, každá hrana odpovídá jedné hodnotě. Každý list pak určuje klasifikaci instance.

ID3 algoritmus

Je algoritmus, který vytváří rozhodovací stromy na základě trénovacích dat. Postupuje top-down -- konstruuje strom od kořene. V každém uzlu si klade otázku: Který atribut je nejlepší pro tento uzel? a řeší ji statistickým testem na základě max. entropie. Počet větví vedoucích z uzlu je počet možných hodnot atributu, takže ho známe hned po vytvoření uzlu. Trénovací data jsou při vytváření dělena podle atributů v daném uzlu.

Pracuje rekurzivně:

Vyřeší singulární případy:
1. Všechna trénovací data jsou pozitivní případy / negativní případy: vytvoří jednouzlové stromy s (+) nebo (-).
2. Nemáme (už) žádné atributy: vytvoří jednouzlový strom s (nejčastější hodnota cíl. funkce v trénovacích datech).
Vybere atribut $ A $, který nejlépe klasifikuje trénovací data a:
1. Pro každou jeho možnou hodnotu udělá poduzel, rozdělí trénovací data podle těchto hodnot.
2. Máme-li pro danou hodnotu atributu trénovací data, volá se rekurzivně (na danou část trénovacích dat a atributy s vynechaným $$ A $$ ).
3. Pokud nejsou trénovací data, vloží list s (nejčastější hodnota cíl. funkce v trénovacích datech).
Vrátí výsledný (pod)strom.

Prochází se celý hypothesis space, ale hladovým způsobem bez backtrackingu. Výstupem je 1 rozhodovací strom, tj. jedna hypotéza.

Výběr nejlepšího atributu probíhá na základě entropie (zisku informace). Který atribut má nejvyšší zisk informace (míra očekávaného snížení entropie), ten je vybrán. Platí: $G(D,A) = H(D) - \sum_{v\in\mathrm{values}(A)}(\frac{|D_v|}{|D|}\cdot H(D_v))$ , kde:

$$ G(D,A) $$ je zisk informace pro data $$ D $$ a atribut $$ A $$ ,
$$ H(D) $$ je entropie dat $$ D $$ vzhledem k cílové funkci,
$$ D_v $$ jsou data, která mají hodnotu atributu $$ A $$ rovnou $$ v $$ .

Vylepšení ID3

Jedním z možných problémů je overfitting. Řekneme, že hypotéza $h\in H$ overfituje trénovací data, pokud existuje alternativní hypotéza $h'\in H$ taková, že $$ h $$ má menší chybu než $$ h' $$ na trénovacích datech, ale na celé distribuci instancí je to naopak.

Vyvarovat se overfittingu lze buď prořezáváním (pruning), např. za použití heldout dat pro validaci při trénování. Pruning je vyříznutí nějakého podstromu. Prořezávat můžeme, pokud je přesnost obecnější hypotézy vyšší než nějaké speciálnější. Postup:

Vyhodit podstrom.
Dát místo něj jeden uzel s (nejčastější hodnota na trénovacích datech) pro podmnožinu odpovídající vyhazovanému podstromu.

Máme víc možností prořezávání, počítáme přesnost a podle toho se rozhodujeme -- je nutné taky vědět, kdy s tím přestat, nutné testovat. K testování se můžou používat heldout data: k prořezání vyberu ten podstrom, jehož vyříznutí nejvíce zlepší úspěšnost na heldout datech.

Strategie rule-post-pruning spočívá v následujícím postupu:

Vytvoření rozhodovacího stromu.
Jeho převedení na pravdila (počet pravidel = počet listů), kdy 1 pravidlo je 1 cesta od listu ke kořeni.
Pro každé pravidlo zahodit ty podmínky, jejichž vyhozením se přesnost pravidla zlepší.
Pravidla setřídit podle přesnosti na trénovacích datech, reálná data klasifikovat použitím pravidel v tomto pořadí.

Proti prořezávání nad stromem nemusíme vyhazovat jen z konce stromu, máme jemnější rozlišení.

Pokud je některý atribut $$ A $$ spojitý (ale cílové ohodnocení stále diskrétní), můžeme ho převést na diskrétní $A_{C}$ : najdeme konstantu $$ C $$ a potom: $A < C \Rightarrow A_{C} = 0$ , $A \geq C \Rightarrow A_{C} = 1$ . Nejlepší $$ C $$ můžeme najít opět pomocí zisku informace:

Zjistíme "přelomové" body, tj. vedle sebe stojící hodnoty, které jsou hodnoceny rozdílně.
Kandidáti na $$ C $$ pak jsou průměry takových to vedle sebe stojících hodnot.
Spočítáme $\overline{C} = \mathrm{argmax}_{C} G(D,A_{C})$ .

Má-li atribut více hodnot (např. nějaké datum), zisk informace ho bude preferovat, což často vede k vytvoření stromu hloubky 1, který funguje jen na trénovací data. Musíme pak změnit test výběru atributů, místo zisku informace používáme ziskový poměr (gain ratio):

Rozštěpení informace (split information): $SI(D,A) = - \sum_{v\in\mathrm{values}(A)}\frac{|D_v|}{|D|}\log_2(\frac{|D_v|}{|D|})$
Ziskový poměr: $GR(D,A) = \frac{G(D,A)}{SI(D,A)}$ , kde $$ G(D,A) $$ je zisk informace pro trénovací data $$ D $$ a atribut $$ A $$

Jsou i jiné způsoby, jak toho dosáhnout.

Pokud jsou některé atributy důležitější než jiné, zavádí se cena atributu (cost of the attribute). Taky se musí vytvořit jiné kritérium, alternativní k zisku informace. Jsou i jiné alternativní způsoby výběru nejlepšího atributu, např. distance-based measure, kdy se vybírá atribut, který dělí data co nejrovnoměrněji podle nějaké metriky (směrodatná odchylka, Gini koeficient). Změna výběru atributů nemá na stromy takový vliv jako prořezávání.

Učení založené na příkladech

Hlavní myšlenka učení založeného na příkladech (instance-based learning): který trénovací příklad je nejbližší aktuální testovací instanci? Mám vždy v paměti celá trénovací data, kdykoliv můžu přidat další a pro každý testovací příklad v nich hledám ty nejpodobnější. Proto je nutné zavést míru závislosti příkladů. My budeme používat euklidovskou míru $d(x,y) = \sqrt{\sum_{i=1}^n (a_i(x) - a_i(y))^2}$ . Cílová funkce může být diskrétní (s def. oborem $V = \{v_1,\dots,v_n\}$ ) nebo spojitá.

K-nearest neighbor

K-nearest neighbor nebo k-nn je algoritmus typu instance-based learning. Počítám s uloženými trénovacími daty $$ E $$ v paměti. Postup pro nějakou testovací instanci $$ x_q $$ :

Je-li $x_q \in E$ , potom mám přímo hodnocení.
Jinak najdu $ k $ nejbližších $ x_1,\dots,x_k\in E $ a:
- Pro diskrétní cílovou funkci $\hat{f}(x_q) = \mathrm{argmax}_{v\in V} \sum_{i=1}^{k} \delta (v, f(x_i))$ , kde $\delta = 1$ pro stejné hodnoty argumentů, a 0 pro různé (tj. přiřadím $$ x_q $$ takovou hodnotu, kterou má nejvíce z oněch $$ k $$ sousedů).
- Pro spojitou cílovou funkci $\hat{f}(x_q) = \frac{\sum_{i=1}^k f(x_i)}{k}$ , tj. udělám průměr hodnocení.

K-nn nikdy nepočítá explicitní obecnou hypotézu, pracuje jen v kontextu. Pro $$ k = 1 $$ de facto odpovídá Voronoi diagramu. Vylepšením může být vážení podle vzdáleností (distance-weighted k-nn), kde:

V diskrétním případě $\hat{f}(x_q) = \mathrm{argmax}_{v\in V} \sum_{i=1}^{k} w_i\cdot\delta (v, f(x_i))$ , kde navíc $w_i = \frac{1}{d(x_q,x_i)^2}$ .
Ve spojitém případě $\hat{f}(x_q) = \frac{\sum_{i=1}^{k} w_i f(x_i)}{\sum_{i=1}^{k} w_i}$ .

Díky vážení můžeme takhle jít dokonce přes celá trénovací data (globální (Shepardova) metoda).

Algoritmus je robustní vzhledem k šumu v trénovacích datech. Problémem je pomalý výpočet vzdáleností ke všem trénovacím datům, pro zrychlení se vytváří indexy, pomocí k-d stromů (vynecháme). Problém je taky, když mám hodně atributů a relevantních jen pár. Pak je metrika vzdáleností zavádějící -- i když se shodují důležité atributy, mohou být od sebe instance "daleko". Řešením je váha atributů.

Lokálně vážená lineární regrese

Lokálně vážená lineární regrese (locally weighted linear regression) je konstrukce lokální aproximace cílové funkce na okolí kolem testovacího příkladu. Používá se často ve statistice. Používají se i jiné než lineární funkce, ale těmi se zabývat nebudeme.

Def.: Regrese je aproximace reálné funkce.
Def.: Reziduum je odchylka aproximace od reálné funkce, tj. $\hat{f}(x) - f(x)$ .
Def.: Jádro (kernel function) je funkce $$ K $$ vzdálenosti $$ d $$ za účelem získání váhy trénovacích příkladů $$ w_i = K(d(x_i, x_q)) $$ . Často je to gaussovská funkce se střední hodnotou $\mu$ a rozptylem $\sigma^2$ .

Aproximace hodnotící funkce je tu ve tvaru: $\hat{f}(x) = w_0 + w_1 a_1(x)+\dots + w_n a_n(x)$ (kde $$ a_i(x) $$ je hodnota $$ i $$ -tého atributu příkladu. Úkolem je pak najít taková $$ w_i $$ , která minimalizují rezidua $E = \frac{1}{2}\sum_{i\in D}(\hat{f}(x)-f(x))^2$ . K tomu slouží algoritmus postupného klesání gradientu (gradient descent training rule) (vynecháme). Aproximace se modifikuje tak, aby byla jen lokální, pro to jsou 3 možnosti (z nichž ta 3. je nejlepší). Nechť $$ NN_k(x_q) $$ je množina $$ k $$ nejbližších sousedů $$ x_q $$ :

$E_1(x_q) = \frac{1}{2}\sum_{x\in NN_k(x_q)} (\hat{f}(x)-f(x))^2$
$E_2(x_q) = \frac{1}{2}\sum_{x\in D}(\hat{f}(x)-f(x))^2\cdot K(d(x_q,x))$ -- tady ale výpočtová složitost závisí na velikosti trénovacích dat $$ |D| $$ .
$E_3(x_q) = \frac{1}{2}\sum_{x\in NN_k(x_q)} (\hat{f}(x)-f(x))^2\cdot K(d(x_q,x))$ -- toto je vhodná aproximace 2. přístupu, výpočetní složitost závisí jen na $$ k $$ .

Bayesovské učení

Tato část je neúplná a potřebuje rozšířit. Tuto kapitolu je třeba upravit, buď s použitím Mitchella, nebo státnicových výcuců, aby nebyla zavádějící

Bayesovské učení (Bayesian learning) je kvantitativní přístup k hypotéze, narozdíl od předchozích se zabývá pravděpodobností. Trénovací příklady tu zvyšují vhodnost (likelihood) nějaké hypotézy. Potřebujeme nějaké apriorní znalosti -- iniciální pravděpodobnosti hypotéz, což je často výpočetně náročné. Klasifikace instancí je založená na hypotézách a jejich pravděpodobnostech, kombinuje se i víc hypotéz.

Při pohledu na strojové učení jako prohledávání prostoru hypotéz k nalezení té nejlepší je pro bayesovské učení nejlepší hypotéza ta nejpravděpodobnější (vzhledem k apriorním pravděpodobnostem a trénovacím datům).

Def.: $$ P(h) $$ -- apriorní pravděpodobnost hypotézy $$ h $$ ; nezávisí na datech
Def.: $$ P(D) $$ -- pravděpodobnost výskytu čehokoliv z trénovacích dat $$ D $$ bez znalosti pravděpodobnosti nějaké hypotézy
Def.: $$ P(D|h) $$ -- podmíněná pravděpodobnost výskytu $$ D $$ , platí-li $$ h $$
Def.: $$ P(h|D) $$ -- aposteriorní pravděpodobnost, pravděpodobnost $$ h $$ za předpokladu, že známe $$ D $$ ; závisí na datech

Zajímá nás právě $$ P(h|D) $$ . Bayesova věta: $P(A|B) = \frac{P(B|A)P(A)}{P(B)}$ , z toho je vidět, že $P(h|D) = \frac{P(D|h)P(h)}{P(D)}$ . Tedy $$ P(h|D) $$ se zvyšuje spolu s $$ P(D|h) $$ a $$ P(h) $$ , ale snižuje s rostoucí $$ P(D) $$ .

Hledáme hypotézu, která má maximální aposteriorní pravděpodobnost (maximální aposteriorní hypotézu), tj. $h_{MAP}=\mathrm{argmax}_{h\in H} P(D|h)P(h)$ (podle Zlatého pravidla). Pokud jsou apriorní pravděpodobnosti všech hypotéz stejné, pak maximálně vhodná hypotéza (maximum likelihood hypothesis) je $h_{ML}=\mathrm{argmax}_{h\in H} P(D|h)$ .

Konceptuální učení hrubou silou

Bayesův vzorec použijeme k algoritmu, který za pomoci vypočtených aposteriorních pravděpodobností ohodnotí hypotézy a vrátí tu nejpravděpodobnější.

Def.: Řekneme, že hypotéza $$ h $$ je konzistentní s trénovacími daty $$ D $$ , pokud $\forall x_i\in D = <x_i,d_i>_{i=1}^n : h(x_i) = d_i$ , tj. ve všech případech na trénovacích datech dává správné ohodnocení.

Pro algoritmus předpokládáme apriorní pravděpodobnost pro všechny hypotézy stejnou, tj. rovnoměrné rozdělení: $P(h) = \frac{1}{|H|}\ \forall h\in H$ . Dále předpokládáme, že $P(D|h) = \begin{cases}1\ \mathrm{pro}\ d_i = h(x_i)\ \forall <x_i,d_i>\in D\\0\ \mathrm{jinak}\end{cases}$ .

Celkový běh algoritmu:

$\forall h\in H: P(h|D) = \frac{P(D|h)P(h)}{P(D)}$
$ h_{MAP} = \mathrm{argmax}_{h\in H} P(h|D) $
1. Je-li $$ h $$ nekonzistentní s $$ D $$ , pak $$ P(D|h) = 0 $$ , proto $$ P(h|D) = 0 $$
2. Je-li $$ h $$ konzistentní s $$ D $$ , pak $$ P(D|h) = 1 $$ , proto $P(h|D) = \frac{1\cdot\frac{1}{|H|}}{\frac{|VS_{H,D}|}{|H|}} = \frac{1}{|H|\cdot P(D)}$ .

To, že $P(D) = \frac{|VS_{H,D}|}{|H|}$ , plyne z věty o úplné pravděpodobnosti: $P(D) = \sum_{i} P(D|h_i)P(h_i)$ , protože $P(h_i\cap h_j) = 0\ i\neq j$ . Potom $P(D) = \sum_{h\in VS_{H,D}} 1\cdot\frac{1}{|H|} + \sum_{h\not\in VS_{H,D}} 0\cdot\frac{1}{|H|} = \frac{|VS_{H,D}|}{|H|}$ .

Z toho a Bayesova vzorce plyne, že $P(h|D) = \begin{cases}\frac{1}{|VS_{H,D}|}\ \mathrm{pro}\ h\ \mathrm{konzistentni\ s}\ D\\0\ \mathrm{jinak}\end{cases}$ . Tedy každá konzistentní hypotéza je maximální aposteriorní, každá konzistentní hypotéza je "nejpravděpodobnější" pro daná trénovací data.

Bayesova optimální klasifikace

Jaká je nejpravděpodobnoější klasifikace nového příkladu? Nemusí být shodná s $h_{MAP}$ . Může-li nabýt libovolné hodnoty $y_j\in Y$ , pak je dána vztahem $P(y_j|D,x) = \sum_{h_i\in H} P(y_j|h_i)P(h_i|D,x)$ a Bayesova optimální klasifikace je to $$ y_j $$ , pro kterou je $$ P(y_j|D,x) $$ maximální (tj. $\mathrm{argmax}$ ).

Libovolný systém, který používá Bayesovu optimální klasifikaci pro nové instance, se nazývá Bayes optimal learning. Tato metoda maximalizuje pravděpodobnost, že nová data budou klasifikována správně za předpokladu trénovacích dat, prostoru hypotéz a apriorních pravděpodobností.

Bayesův optimální klasifikátor poskytuje sice nejlepší možné výsledky z trénovacích dat, ale je výpočetně náročný. To motivuje použití Gibbsova algoritmu:

Vybere se náhodně $h\in H$ vzhledem k distribuci aposteriorních pravděpodobností nad $$ H $$ .
$$ h $$ se použije k predikci klasifikace nové instance.

Naive Bayes Classifier

Menší výpočetní náročnost než optimální bayesovská klasifikace má i Naivní bayesovský klasifikátor. Ten lze použít, když každou instanci lze popsat $$ n $$ -ticí hodnot atributů a cílová funkce $$ c(x) $$ nabývá hodnot z konečné množiny $$ Y $$ .

Bayesovský přístup: $y_{MAP} = \mathrm{argmax}_{y\in Y} P(y|a_1,\dots,a_n) = \mathrm{argmax}_{y\in Y} P(a_1,\dots,a_n|y)P(y)$ . Použijeme:

$$ P(y) $$ je relativní frekvence výskytu $$ y $$ v trénovacích datech.
$P(a_1,\dots,a_n|y) = \prod_{i=1}^n P(a_i|y)$ , tj. předpokládáme nezávislost hodnot atributů (zjednodušení Naivního klasifikátoru).

Ve výsledku $y_{NBC} = \mathrm{argmax}_{y\in Y} P(y)\prod_{i=1}^n P(a_i|y)$ .

Je-li splněn předpoklad o podmíněné nezávislosti hodnot atributů, je $y_{NBC} = y_{MAP}$ . Nevyžadujeme ale prohledávání všech možných hypotéz (tj. možných hodnot $$ P(y) $$ a $$ P(a_i|y) $$ ), jen počítáme frekvence specifických jevů v trénovacích datech.

Délka minimálního popisu

Délka minimálního popisu (minimum description length) souvisí s Occamovou břitvou. Platí totiž:

 $h_{MAP} = \mathrm{argmax}_{h\in H} P(D|h)P(h) = \mathrm{argmax}_{h\in H}\log_2 P(D|h) + \log_2 P(h) =$ 
 $= \mathrm{argmin}_{h\in H} - \log_2 P(D|h) - \log_2 P(h)$

A to se dá interpretovat jako preference nejkratší hypotézy s ohledem na specifický systém reprezentace hypotéz a dat. Pokud označíme $$ L_C(i) $$ počet bitů potřebných k zakódování zprávy $$ i $$ v kódování $$ C $$ , pak se dá vzorec přepsat jako $h_{MAP} = \mathrm{argmin}_h L_{C_h}(h) + L_{C_{D|h}} (D|h)$ (uvažujeme optimální kódování prostoru hypotéz i trénovacích dat s ohledem na hypotézu $$ h $$ ).

Princip délky minimálního popisu je následující:

Vyber $h_{MDL}$ takové, že $h_{MDL} = \mathrm{argmin}_{h\in H} L_{C_1}(h) + L_{C_2}(D|h)$ .

Pokud je $$ C_1 $$ optimální kódování hypotéz a $$ C_2 $$ optimální kódování trénovacích dat, pak $h_{MAP} = h_{MDL}$ .

Přesto z toho nevyplývá, že nejkratší hypotézy jsou nejlepší.

Vyhodnocování hypotéz

Tato část je neúplná a potřebuje rozšířit. dopsat

Support Vector Machines

Tato část je neúplná a potřebuje rozšířit. dovysvětlit "(?)", celkově líp vysvětlit

Do 80. let většina algoritmů pro strojové učení používala lineární funkce. V 80. letech přišly algoritmy jako k-nn nebo rozhodovací stromy, které používaly nelineární rozhodovací plochy. Od 90. let už za algoritmy stojí silné teoretické pozadí, což platí i o SVM. Nepřistupujeme tu k učení jako k problému vyhledávání, nýbrž optimalizace.

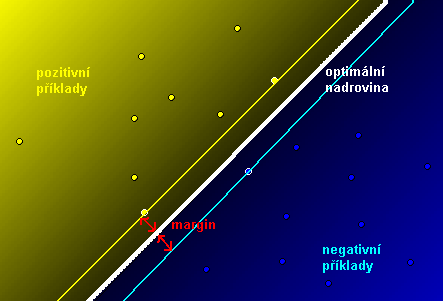
Support vector machine a optimální nadrovina

SVM lze použít, pokud máme hodnoty atributů jednotlivých příkladů spojité. Pak můžeme zkonstruovat pomocí kernelové funkce prostor atributů (feature space). V něm jsou umístěny jednotlivé příklady a my hledáme nejlepší nadrovinu, která odděluje negativní příklady od pozitivních (tj. máme optimalizační problém). Nejlepší nadrovina je taková, která má největší margin (vzdálenost k nejbližší rovnoběžce, která prochází nějakými příklady, viz obrázek).

Každou nadrovinu můžeme popsat rovnicí $\mathbf{w}\times\mathbf{x}-b = 0$ (kde $\times$ je skalární součin), $\mathbf{w}$ je její normálový vektor. Popíšeme hraniční nadroviny (support vectors; rovnoběžky s nadrovinou, které se dotýkají pozitivních, resp. negativních příkladů) jako $\mathbf{w\times x}-b =1$ a $\mathbf{w\times x}-b=-1$ . Podle vzorce pro vzdálenost z geometrie je vzdálenost nadroviny od hraničních nadrovin $d = \frac{|\mathbf{w\times x}-b|}{\sqrt{||\mathbf{w}||^2}} = \frac{1}{||\mathbf{w}||}$ , celková vzdálenost (margin) je tedy $\frac{2}{||\mathbf{w}||}$ . Tedy k maximalizování marginu musíme minimalizovat $\mathbf{w}$ . K tomu máme další podmínky, aby se hraniční nadroviny dotýkaly právě nejbližších případů k nadrovině.

Úloha maximalizace marginu je vlastně úloha kvadratického programování -- máme:

Maximalizační kritérium $\mathrm{argmin}\frac{1}{2}||\mathbf{w}||^2$ (výsledek je stejný jako u minimalizace $\mathbf{w}$ , ale kritérium je kvadratické).
Nerovnice (zajišťují to, že nadrovina je na správné straně od všech bodů) tvaru $\mathbf{w \times x}_i + b\geq 1$ pro pozitivní případy a $\mathbf{w\times x}_i + b\leq -1$ pro negativní.
Rovnice (zajišťují, že mám opravdu nadrovinu (?)) $\mathbf{wx}+b=0$

To se dá přepsat do duálního tvaru v kvadratickém programování:

Maximalizovat $\mathrm{max}\sum_{i=1}^n\alpha_i -\frac{1}{2}\sum_{i,j}\alpha_i\alpha_j c_i c_j\mathbf{x}_i^T\mathbf{x}_j$
Za podmínky $\alpha_i \geq 0$ a $\sum_{i=1}^n \alpha_i c_i = 0$

Kde $\mathbf{w} = \sum_i\alpha_i c_i\mathbf{x}_i$ ( $$ c_i $$ odlišuje nadroviny příslušející pozitivním příkladům od těch k negativním, je buď rovné $$ -1 $$ nebo $$ 1 $$ ).

Většina parametrů je nulová (jde jen o instance nejbližší dělící nadrovině, tzv. borders), takže dostanu řešení s velmi malým počtem parametrů.

Chování SVM můžu ovlivňovat dvěma věcmi: pomocí slack variables a transformací feature space.

Slack variables

Kvůli špatně klasifikovaným datům (pro větší robustnost) existuje úprava za pomocí slack variables (korigující míry, pro správně klasifikovaná data jsou nulové). Potom se minimalizuje $\frac{1}{2}||\mathbf{w}||^2 + C\cdot\sum_i\xi_i$ , kde $\xi_i$ jsou slack variables a $$ C $$ je konstanta určující velikost penalizace špatně klasifikovaných dat.

Transformace feature space

S jednotlivými atributy můžeme dělat polynomiální transformace a kombinovat je, např. máme-li $$ h, w $$ jako výšku a šířku, můžeme je upravit na $h, w, h\cdot w, h^2, w^2$ pro polynomiální transformace do stupně 2. V praxi se vyšší než stupeň 3 většinou nepoužívá. Problém ale je stále lineární, mění se jen prostor atributů!

Další transformace jsou např. radial basis function (něco jako hustota normálního rozdělení) -- $\exp\{c\cdot ||\mathbf{x-x'}||^2\}$ . Parametry si musím zjistit sám podle konkrétního případu. Podobná je i Gaussian basis function, která vypadá podobněji Gaussově definici hustoty normálního rozdělení.

Více hodnot cílové funkce

Pokud má cílová funkce $$ n $$ hodnot místo dvou, jsou tu dvě strategie:

1-versus-all -- definuju funkce = nadroviny dělící prostor na $$ + $$ a $$ - $$ (mám $$ n $$ funkcí) tím, že vezmu vždycky jednu třídu a zbytek považuju za druhou třídu. Pak klasifikuju nové instance k té třídě, která má nejbližší nadrovinu.
1-versus-1 -- pro každý pár hodnot mám jednu funkci, tj. nakonec jich je ${n \choose 2}$ .