Státnice - Metody tvorby algoritmů I2
Tohle je poněkud obšírnější výcuc ke státnicovým okruhům ze složitosti pro obor Softwarové systémy, pocházející ze zápisků z předmětu Složitost I a Státnice_-_Metody_tvorby_algoritmů
Amortizovaná složitost (🎓)
| Zážitky ze zkoušek |
|---|
|
Asymptotická složitost - složitost pro jednu operaci
- asymptoticky ≤ -- f(n) je O(g(n)) ⇔ ∃c>0 ∃n₀ ∀n ≥ n₀: 0 ≤ f(n) ≤ c.g(n)
- asymptoticky ≥ -- f(n) je Ω(g(n)) ⇔ ∃c>0 ∃n₀ ∀n ≥ n₀: 0 ≤ c.g(n) ≤ f(n)
- asymptoticky = -- f(n) je Θ(g(n)) ⇔ ∃c₁,c₂>0 ∃n₀ ∀n ≥ n₀: 0 ≤ c₁.g(n) ≤ f(n) ≤ c₂.g(n)
Amortizovaná složitost - pro posloupnost operací
- Typické použití pro odhad časové složitosti posl. operací na dat. struktuře
- Počítá amortizovanou cenu (průměrný čas na 1 operaci při provedení posloupnosti op) každé operace v nejhorším případě(v nejhorší možné posloupnosti operací)
- Dává realističtější odhad slož, než klasický odhad složitosti každé operace nejhořším možným případem
- Nejedná se o složitost v průměrným případě
Amortizovaná analýza:
- Agregační metoda - Spočítáme nejhorší možný čas T(n) pro posl. N operací. Amortizovaná cena 1 op je pak T(n)/n
- Účetní metoda - Od každé op. Vybereme určitý peněžný obnost, ze kterého zaplatíme za danou operaci. Jedna jednotka stačí na konstatní množství práce. Pokud po zaplacení nějaké peníe zbudou, jdou na "účet". Pokud pro zaplacení operace nějaké peníze chybí, tak lze z účtu čerpat. Účet musí být pořád v nezáporny.
Příklad 1: Inkrementace bin. čítače.
- k-bit binární čítač, všude 0, pak ho nkrát inkrementujem (cíl je spočítat bitové operace (bit-flipy) na jednu inkrementaci.
- Klasicky počítaný nejhorší případ: n inkrementací a log n bit-flipů na jednu inkrementaci v nejhorším případě -> celkem O(n log n) bitflipů
- Ukážeme, že amortizovaná cena jedné inkrementace je 2 = O(1) a tímpádem je celkový počet bitflipů jen O(n)
D(účetní): Každá inkrementace změní právě jeden bit z 0 na 1 -> 1 peníz za flip, druhý do banky (každý byt, jež má 1 má 1 peníz v bance) -> ten se použije v momentě, kdy se má změnit z 1 na 0.
D (agregační): l = [ log n ] dolní celá část. V průběhu n flipů se 0 tý byt překlopí nkrát, 1ní - n/2 krát (dcč), 2hý- n/4 atd....
Suma vyjde =2n -> Amortizovaná cena 1 přičtění je 2n/n = 2 = 2 O(1)
Příklad 2: Vkládání do dynamického pole:
Prázdné pole s délkou 1 a postupně do něj vložíme n prvků. Pokud je pole plné vytvoří se 2násobné a zkopíruje se současné. Cíl:Spočítat operace s prvky pole na jedno vložení.
- Klasicky v nejhorším případě: n vložení a O(n) opearací s prvky pole na jedno vložení v nejhorším případě -> O(n2) operací s prvky pole
- Amortizovaán složitost jednoho vložení je 3 = O(1) a tím pádem je celkový počet operací s prvky pole jenom O(n).
D (agregační): cena i-tého vložení ci = i (pokud existuje K: i-1=2k) jinak 1.
Celková cena n vložení je suma ci = n + Suma (j=0..log n) 2j <= n+ 2n = 3n.
Amortizovaná složitost je 3n/n = 3 = O(1)
D (účetní): 3. Jedna na vložení, při expanzi druhá polovina pole platí kopii celého pole, proto každý prvek potřebuje 2 penízky.
Metody tvorby algoritmu: rozdel a panuj, dynamické programování, hladový algoritmus.
Rozděl a panuj (🎓)
| Zážitky ze zkoušek |
|---|
|
Rozděl a panuj je metoda návrhu algoritmů, která má 3 kroky (+ vytvoření rekurentní rovnice):
- rozděl -- rozdělí úlohu na a (nezávislých) podúloh stejného typu velikosti n/c ( doba D(n) )
- vyřeš -- vyřeší podúlohy a to buď přímo pro dostatečně malé, nebo rekurzivně pro větší ( doba T(n/c) )
- sjednoť -- sjednotí řešení podúloh do řešení původní úlohy velikosti n ( doba S(n) )
⇒ rekurentní rovnice T(n) = D(n) + aT(n/c) + S(n) (pro triviální n je to celé Θ(1))
Analýza časové složitosti (2 metody řešení):
- substituční metoda - uhodneme správné řešení a indukcí jej ověříme (zvlášť shora a zvlášť zdola)
- "kuchařka" (Master Theorem)
Master Theorem (mnemotechnicky)
Nechť a ≥ 1, b > 1, c ≥ 0 ∈ ℝ a nechť T : ℕ → ℕ je neklesající fce taková, že pro ∀n ve tvaru bᵏ (kde k ∈ ℕ) platí
T(n) = aT(n/b) + Θ(nc)
Potom
- je-li a > bc, potom platí T(n) = Θ(nlogb a) (práce přibývá cestou dolů ve stromu rekurze, tedy ~ #listů stromu)
- je-li a < bc, potom platí T(n) = Θ(nc) (práce ubývá cestou dolů ve stromu, tedy ~ původní práci v kořenu)
- ☀ spojení do 1: a ≠ bc, potom platí T(n) = Θ(nmax{logb a, c}),
- je-li a = bc, potom platí T(n) = Θ(nc logb n) (práce stejná cestou dolů ve stromu, tedy ~ hloubce stromu × práce na ∀úrovni)
Aplikace
- Mergesort (rozdel na pulky az do delky 1 a pak slevej monotonni posloupnosti)
- T(n) = 2T(n/2) + Θ(n) ⇒ Θ(n log n)
- QUICKSORT
- nejhorší složitost - pivot špatně: T(n)=T(n-1)+Ө(n) = Ө(n2)
- průměr složitost - pivot náhodně: O(n log n)
- nejlepší složitost - pivot medián: T(n)=2T(n/2)+O(n) ⇒ a=2 b=2 c=1 ; 2=21 ⇒ Ө(n log n)
- Hledání mediánu v linearnim case (pomoci pivotu rozdelujeme posloupnost tak dlouho, nez mame prostredni prvek. pivot vybirame pomoci rozdeleni na petice a vyber medianu z medianu petic. median z medianu je poduloha, median z petice trivialita)
- T(n) = c . n/5 + T(n/5) + (n-1) + T(7/10) → Θ(n)
Poznámky:
- oproti dynamickému prg. dělá více práce na podproblémech a proto je více časově náročná (shora dolů)
- u Rozděl a panuj jsou podproblémy navzájem nezávislé
| další zdroje |
|---|
Dynamické programování (7×🎓)
| pomalý (exponenciální) rekurzivní alg.: | |
|---|---|
function Fibonacci(n: integer): integer;
begin
if n <= 2 then
Fibonacci := 1
else
Fibonacci := Fibonacci(n-1) + Fibonacci(n-2)
end;
|
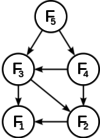
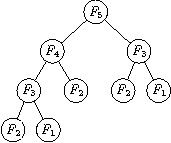
strom volání pro F₅: |
| Zážitky ze zkoušek |
|---|
|
je metoda řešení komplexních problémů, využíváme v něm:
- Překrývání podproblémů - problém lze rozdělit na podproblémy, jejichž řešení se využívá opakovaně
- tj. subproblémy jsou závislé narozdíl od Rozděl a panuj
- řeší subproblémy pouze jednou a pak je většinou uloží do tabulky (aby se výsledky daly znovu použít)
- Optimální podstruktury - optimální řešení lze zkonstruovat z optimálních řešení podproblémů.
- 💡 pro srovnání: hladové algoritmy používají jenom optimální podstruktury
💡 prakticky je to technika, kterou jde z pomalého rekurzivního algoritmu vyrobit pěkný polynomiální (až na výjimečné případy)
Příklad pro výpočet Fibonacciho čísla
Fib. posloupnost je definována jako:
- f(0) = 1, f(1) = 1
- f(n+2) = f(n+1) + f(n)
Výpočet třeba 4. čísla by pak byl f(4) = f(3) + f(2) = f(2) + f(1) + f(1) + f(0) = f(1) + f(0) + f(1) +f(1) +f(0) = 5. Vidíme, že jsme f(2) počítali dvakrát, f(1) třikrát a f(0) dvakrát. Ve větším měřítku toto zbytečně počítání vede k exponenciální složitosti algoritmu. Lepší cestou je počítat "od spodu", kdy pomoci f(0) a f(1) spočteme f(2), pak s jeho pomoci f(3) nakonec f(4) s lineární složitosti.
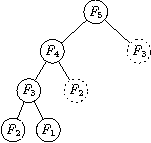
V dynamickém programování se například vytvoří mapa Fibonacciho čísel a jejich hodnot. Před tím, než začnu počítat hodnotu nějakého Fibonacciho čísla, se podívám do mapy.
Přístupy
Obvykle se používá jeden ze dvou přístupů k dynamickému programování:
Top-down
|
Bottom-up
function Fibonacci(n: integer): integer;
var
P: array[1..MaxN] of integer;
i: integer;
begin
P[1] := 1;
P[2] := 1;
for i := 3 to n do
P[i] := P[i-1] + P[i-2];
Fibonacci := P[n]
end;
|
Hladové algoritmy (🎓)
| Zážitky ze zkoušek |
|---|
|
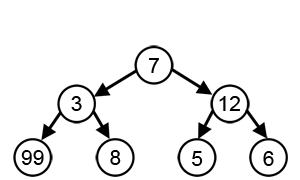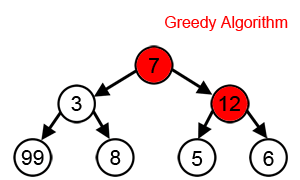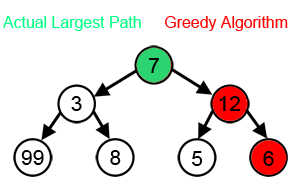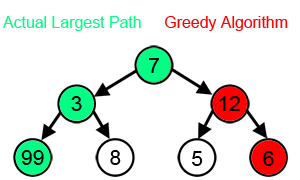
"Dokud můžeš, neohlížej se a jdi rovnou za nosem." neboli splňují tyto 2 podmínky:
- Optimální podstruktury - V každém kroku zvolí lokálně nejlepší řešení.
- Žádný backtracking - Provedené rozhodnutí již nikdy neodvolává (tedy nebacktrackuje).
Pokud ale od hladového algoritmu chceme, aby nám našel globálně nejlepší řešení, musí naše úloha splnit předpoklad, že si výběrem lokálně nejlepšího řešení nezhoršíme to globální. Tento předpoklad se nedá formulovat obecně a je nutné se nad ním zamyslet zvlášť u každé úlohy.
hladový algoritmus
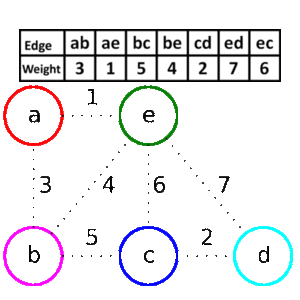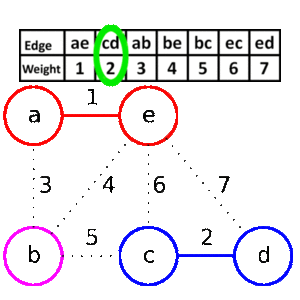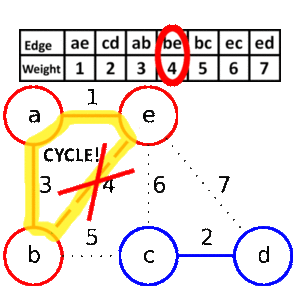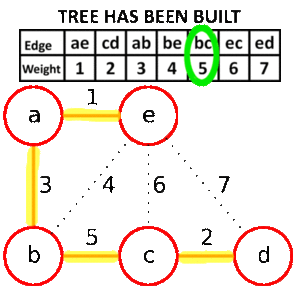
- setridime mnozinu podle velikosti
- vybirame od prvniho prvku do posledniho. Kazdy novy prvek, ktery neporusi integritni omezeni (napr. u hledani minimalni kostry pokud novy vrchol uzavre nejakou kruznici a tudiz by vybrana mnozina nebyla kostrou) pridame do vybrane mnoziny
Př. Automat na colu
První hladovou úlohou bude (jak jinak) automat na jídlo vracející mince. Automat by měl vracet peníze nazpět tak, aby vrátil daný obnos v co možná nejmenším počtu mincí. Pro náš měnový systém (máme mince hodnot 1, 2, 5, 10, 20 a 50 Kč) lze tuto úlohu řešit hladovým algoritmem – v každém kroku algoritmu vrátíme tu největší minci, kterou můžeme (tedy pro vrácení 42 Kč to bude 42 = 20 + 20 +2 Kč).
Měnové systémy většiny států jsou postavené tak, aby fungovaly takto pěkně, neplatí to ale obecně. Zkusme si vrátit 42 Kč, pokud bychom měli jen mince hodnoty 20, 10 a 4 Kč. Správným řešením je 42 = 20 + 10 + 4 + 4 +4 Kč, hladový algoritmus by ale zkusil vrátit 42 = 20 + 20 + … a tady by selhal.
| další zdroje |
|---|
|
https://ksp.mff.cuni.cz/tasks/27/cook1.html#Hladov%C3%A9%20algoritmy |
Státnice -- Softwarové systémy
Složitost a vyčíslitelnost -- Tvorba algoritmů (10🎓), NP-úplnost (15🎓), Aproximační algoritmy (6🎓), Vyčíslitelné funkce a rekurzivní množiny (8🎓), Nerozhodnutelné problémy (9🎓), Věty o rekurzi (6🎓)
Datové struktury -- Stromy (32🎓), Hašování (13🎓), Třídění (10🎓)
Databázové systémy -- Formální základy: Relace (12🎓), Datalog (9🎓), Ostatní (0🎓) Modely a jazyky: SQL (7🎓), DIS (7🎓), Odborné (3) Implementace: Transakce (5🎓), Indexace (10🎓), Komprese (3)
Softwarové inženýrství -- Programovací jazyky a překladače, Objektově orientované a komponentové systémy, Analýza a návrh softwarových systémů
Systémové architektury -- Operační systémy, Distribuované systémy, Architektura počítačů a sítí
Počítačová grafika -- Geometrické modelování a výpočetní geometrie, Analýza a zpracování obrazu, počítačové vidění a robotika, 2D počítačová grafika, komprese obrazu a videa, Realistická syntéza obrazu, virtuální realita
🎓 - znamená kolikrát byla otázka u státnic