Státnice - Stromové vyhledávací struktury
Tohle je poněkud obšírnější výcuc ke státnicovým okruhům z datových struktur, z různých zápisků k předmětu Datové struktury I, OZD I a výtahů k bakalářským státnicím -- Tuetschek 00:13, 18 Aug 2010 (CEST)
Binární vyhledávací stromy
Definice
Binární vyhledávací strom $ T\,\! $ reprezentující množinu prvků $ S\,\; $ z (uspořádaného) univerza $ U\,\; $ je úplný strom (tj. všechny vnitřní vrcholy mají 2 syny), ve kterém existuje bijekce mezi množinou $ S\,\! $ a vnitřními vrcholy taková, že pro $ v\,\! $ vnitřní vrchol stromu platí:
- všechny vrcholy podstromů levého syna jsou $ \leq v\,\! $
- všechny vrcholy podstromů pravého syna jsou $ >v\,\! $.
Listy reprezentují jednotlivé intervaly mezi vnitřními vrcholy. Můžeme je vynechat, ale s nimi je to (jak pro koho) logičtější.
Základní operace na stromech
- MEMBER -- test, zda prvek $ x\,\; $ je obsažen ve stromě (vyhledání, zpravidla s využitím invariantu )
- INSERT -- vložení prvku $ x\,\; $ do stromu
- DELETE -- odebrání prvku $ x\,\; $ ze stromu
- MIN, MAX, ORD -- nalezení prvního, posledního, $ k\,\! $-tého největšího prvku
- SPLIT -- rozdělení stromu podle $ x\,\! $, které vyhodí, je-li ve stromě
- JOIN -- spojení dvou stromů (jsou dvě verze, s přidáním prvku navíc, nebo bez něho)
Obecná (nevyvážená) implementace
- INSERT: najít list reprezentující interval, kam vkládám, udělat z něj normální uzel se vkládanou hodnotou a dát mu dva listy s podintervaly.
- DELETE: najdu vrchol, má-li jednoho syna-lista, pak druhý syn ho nahradí na jeho místě, jinak najdeme a dáme na jeho místo nejmenší větší vnitřní vrchol, jehož levý syn je list, a pravého syna tohoto vrcholu dáme na jeho místo.
- SPLIT: procházím stromem a hledám $ x\,\! $, ost. prvky házím cestou do dvou stromů $ T_1,T_2\,\! $, ve kterých si vždy uchovávám ukazatel na list, místo kterého vkládám (odkrojím syna, ve kterém hledám dál, místo něj vložím list, na který si pamatuju ukazatel).
- JOIN: s prvkem navíc, triviální -- spojím stromy jako 2 syny nového prvku.
Tato struktura sama nepodporuje efektivní ORD, je nutné přidat navíc položky, které určují počet listů v podstromu každého vrcholu. ORD je pak jen jde do pravých synů a přičítá levé podstromy když může, jinak jde do levého syna (a nepřičte nic).
Analýza algoritmů
Definujme si pomocné hodnoty $ \lambda,\pi\,\! $ jako hodnoty nejbližšího menšího (levějšího), resp. většího (pravějšího) prvku na vyšší úrovni, nebo $ -\infty\,\! $, resp. $ +\infty\,\! $, pokud tyto prvky neexistují.
Korektnost vyhledávání: Je-li $ T'\,\! $ podstrom $ t\in T\,\! $, pak $ T'\,\! $ reprezentuje $ S\cap(\lambda(t),\pi(t))\,\! $ (a je to největší interval nezastoupený mimo $ T'\,\! $). Pak pro vyhledání vrcholu $ x\,\! $ platí $ \lambda(t)<x<\pi(t)\,\! $, vyšetřuji-li vrchol $ t\,\! $.
Díky tomu je korektní MEMBER a INSERT. U DELETE musím dokázat korektnost případu s přehazováním vrcholů (dostávám bin. strom reprezentující $ S\setminus\{x\}\,\! $).
Korektnost MIN, MAX, JOIN je zřejmá, u SPLIT plyne z korektnosti hledání a toho, že moje označené listy jsou nejlevější, resp. nejpravější.
Korektnost ORD plyne z toho, že v každém kroku je $ k\,\! $-tý prvek představován tolikátým v pořadí vrcholů akt. vyšetřovaného podstromu, kolik mi zbývá přičíst.
Složitost: Zpracování 1 vrcholu je vždy $ O(1)\,\! $ a alg. se pohybuje po nějaké cestě od kořene k listu, která má $ O(h)\,\! $, kde $ h\,\! $ je výška stromu.
Vyvažování
Chceme-li pro zachování efektivity operací zajistit, že výška bude $ O(\log|S|)\,\! $, přidáme pro strom další podmínky, které bude muset splňovat a operace je zachovávat.
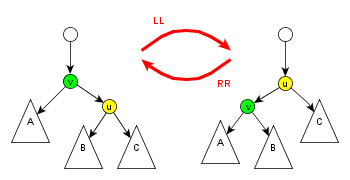
Pro vyvažovací operace, které se snaží zachovat logaritmickou výšku, se používá pomocný algoritmus ROTACE$ (u,v)\,\! $:
- Vezmu $ v\,\! $, jeho pravého syna $ u\,\! $ a podstromy (zleva) $ A,B,C\,\! $.
- Přehodím $ v\,\! $ pod $ u\,\! $, upravím ukazatel v otci a přeházím podstromy.
Existuje i symetrický případ, kdy se postupuje přesně opačným směrem. Někdy se této dvojici operací říká LL-ROTACE a RR-ROTACE.
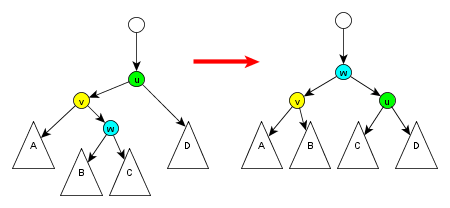
Další potřebný algoritmus je DVOJROTACE$ (u,v,w)\,\! $:
- Vezmu $ u\,\! $, jeho levého syna $ v\,\! $ a pravého syna $ v\,\; $ -- $ w\,\! $
- Seřadím je tak, že $ w\,\! $ je otec obou, $ u\,\! $ vpravo a $ v\,\! $ vlevo.
- Přitom opět upravím ukazatele v nadřízeném uzlu a přepojím podstromy.
Taky existuje symetrický případ. Jiné označení je LR-ROTACE a RL-ROTACE.
U obou operací lze aktualizovat i počty listů v podstromě a obě pracují v $ O(1)\,\! $.
Alternativy k vyvažování
Je velká pravděpodobnost, že i bez vyvažování strom zůstane $ O(\log|S|)\,\! $ vysoký a operace na něm můžou tak (bez vyvažování) běhat i rychleji. Proto existují i pravděpodobnostní postupy, nahrazující vyvažování znáhodněním posloupností operací. Další možnost jsou samoopravující struktury -- operace samy bez dalších uchovávaných dat obstarávají vyvažování, existuje strategie, která zajistí dobré chování bez ohledu na data. Nebo se sleduje chování struktury, a když začne být příliš pomalá, vytvoří se nová -- vyvážená. Poslední možnost je upravit dat. strukturu podle známého pravděpodobnostního rozdělení dat.
AVL-stromy
AVL-stromy (Adel'son-Velskii, Landis) jsou nejstarší vyvážené stromy, dodnes oblíbené, jednoduše definované, ale detailně technicky složité.
Podmínka AVL pro vyvažování: Výška pravého a levého podstromu lib. vrcholu se liší max. o 1.
Definice: $ \eta(v)\,\! $ -- výška vrcholu (délka nejdelší cesty z vrcholu do listů), $ \omega(v)\,\! $ -- rozdíl výšek levého a pravého podstromu ($ \in\{-1,0,1\}\,\! $). Uchovávat potřebuji jenom $ \omega\,\! $.
Logaritmická výška
Výška celého stromu ($ \eta(\,\! $kořen$ )\,\! $) vychází z toho, že podstrom AVL stromu je vždy AVL strom. Vezmeme rekurzivní vztahy pro největší a nejmenší množinu uzlů v AVL stromu výšky $ i\,\! $:
- Nejmenší: $ mn(i)=mn(i-1)+mn(i-2)+1\,\! $
- Největší: $ mx(i)=2mx(i-1)+1\,\! $
Indukcí dokážeme, že $ mx(i)=2^i-1\,\! $ a $ mn(i)=F_{i+2}-1\,\! $, kde $ F_i\,\! $ je $ i\,\! $-té Fibonacciho číslo (pro ty platí vzorec $ F_{i+2}=F_{i+1}+F_{i}\,\! $). Víme, že $ \lim_{i\to\infty}F_i= \sqrt{5}(\frac{1+\sqrt{5}}{2})^{-i}\,\! $ a z toho zlogaritmováním plyne pro AVL-strom o výšce $ i\,\! $ s $ n\,\! $ prvky:
- $ \log\left(\frac{c_1}{\sqrt{5}}\right)+(i+2)\log\left(\frac{1+\sqrt{5}}{2}\right)<\log(n+1)<i\,\! $
A tedy $ 0.69i<\log(n+1)<i\,\! $, takže $ i=\Theta(\log n)\,\! $.
Operace na AVL stromech
Operace MEMBER je stejná jako pro nevyvážené.
INSERT se musí po běžném vložení zabývat vyvažováním. Jde zpět ke kořeni a hledá, který nejnižší vrchol $ x\,\! $ nemá po vložení vyvážené $ \omega\,\! $, přičemž cestou upravuje $ \omega\,\! $. Na vrcholu $ x\,\! $ se provede vhodná ROTACE nebo DVOJROTACE, což zajistí vyváženost (existuje několik podpřípadů).
Operace DELETE odstraní vrchol a pak vyvažuje podobně jako INSERT, ale potřebuje víc operací (až $ O(\log|S|)\,\! $ rotací). Asymptotická složitost je ale stejná -- logaritmická.
Červeno-černé stromy
Červeno-černý strom má tyto čtyři povinné vlastnosti:
- Každý uzel má definovanou barvu, a to černou nebo červenou.
- Každý list je černý.
- Každý červený vrchol musí mít oba syny černé.
- Každá cesta od libovolného vrcholu k listům v jeho podstromě musí obsahovat stejný počet černých uzlů. Pro červeno-černé stromy se definuje černá výška uzlu ($ \mathbf{bh}(x)\,\! $) jako počet černých uzlů na nejdelší cestě od uzlu k listu.
Garantování výšky
Podstrom libovolného uzlu $ x\,\! $ obsahuje alespoň $ 2^{\mathbf{bh}(x)}-1\,\! $ interních uzlů. Díky tomu má červeno-černý strom výšku vždy nejvýše $ 2\log(n+1)\,\! $ (kde $ n\,\! $ je počet uzlů). (Důkaz prvního tvrzení indukcí podle $ \mathbf{h}(x)\,\! $, druhého z prvního a třetí vlastnosti červeno-černých stromů)
Algoritmy
U algoritmů INSERT a DELETE jde také o vložení a následné vyvažování. Bez porušení vlastností červeno-černých stromů lze kořen vždy přebarvit načerno, můžeme pro ně předpokládat, že kořen stromu je vždy černý.
INSERT vypadá následovně:
- Vložený prvek se přebarví načerveno.
- Pokud je jeho otec černý, můžeme skončit -- vlastnosti stromů jsou splněné. Pokud je červený, musíme strom upravovat (předpokládejme, že otec přidávaného uzlu je levým synem, opačný připad je symetrický):
- Je-li i strýc červený, přebarvit otce a strýce načerno a přenést chybu o patro výš (je-li děd černý, končím, jinak můžu pokračovat až do kořene, který už lze přebarvovat beztrestně).
- Je-li strýc černý a přidaný uzel je levým synem, udělat pravou rotaci na dědovi a přebarvit uzly tak, aby odpovídaly vlastnostem stromů.
- Je-li strýc černý a přidaný uzel je pravým synem, udělat levou rotaci na otci a převést tak na předchozí případ.
DELETE se provádí takto:
- Skutečně odstraněný uzel (z přepojování -- viz obecné vyhledávácí stromy) má max. jednoho syna. Pokud odstraňovaný uzel byl červený, neporuším vlastnosti stromů, stejně tak pokud jeho syn byl červený -- to řeším přebarvením toho syna načerno.
- V opačném případě (tj. syn odebíraného -- $ x\,\! $ -- je černý) musím udělat násl. úpravy (předp., že $ x\,\! $ je levým synem svého nového otce, v opačném případě postupuji symetricky):
- $ x\,\! $ prohlásím za "dvojitě černý" ("porucha") a této vlastnosti se pokouším zbavit.
- Pokud je (nový) bratr $ x\,\! $ (buď $ w\,\! $) červený, pak má 2 černé syny -- provedu levou rotaci na rodiči $ x\,\! $, prohodím barvy rodiče $ x\,\! $ a uzlu $ w\,\! $ a převedu tak situaci na jeden z násl. případů:
- Je-li $ w\,\! $ černý a má-li 2 černé syny, prohlásím $ x\,\! $ za černý a přebarvím $ w\,\! $ načerveno, rodiče přebarvím buď na černo (a končím) nebo na "dvojitě černou" a propaguji chybu (mohu dojít až do kořene, který lze přebarovat beztrestně).
- Je-li $ w\,\! $ černý, jeho levý syn červený a pravý černý, vyměním barvy $ w\,\! $ s jeho levým synem a na $ w\,\! $ použiji pravou rotaci, čímž dostanu poslední případ:
- Je-li $ w\,\! $ černý a jeho pravý syn červený, přebarvím pravého syna načerno, odstraním dvojitě černou z $ x\,\! $, provedu levou rotaci na $ w\,\! $ a pokud měl původně $ w\,\! $ (a $ x\,\! $) červeného otce, přebarvím $ w\,\! $ načerveno a tohoto (teď už levého syna $ w\,\! $) přebarvím načerno.
MIN a MAX jsou stejné jako pro nevyvážené.
JOIN (s prvkem navíc): mám-li černou výšku u obou stejnou, není co řešit, pokud ne, projdu po tom s větší $ \mathbf{bh}(x)\,\! $ do patra, kde se výšky rovnají, půjčím si přísl. podstrom a slepím s ním, vrátím celek zpátky a aplikuji vyvažování, jako kdybych vložil 1 prvek (poruším výšku max. o 1).
SPLIT: rozhazuji podstromy do zásobníků, odkud je pak slepuji operací JOIN.
Každý algoritmus pracuje jen s vrcholy na jedné cestě od kořene k listům a s každým dělá konstantně činností, takže všechny algoritmy mají logaritmickou složitost. DELETE volá max. 2 rotace nebo 1 rotaci a 1 dvojrotaci, INSERT zase max. 1 rotaci nebo dvojrotaci (i když přebarvovat můžou rekurzivně až do kořene).
Váhově vyvážené stromy (BB-α)
Dnes jsou už na ústupu, ale občas se ještě používají. Mějme $ 1/4<\alpha<1-\sqrt{2}/2\,\! $, označme $ p(T)\,\! $ počet listů ve stromě $ T\,\! $. Pak strom je BB-$ \alpha\,\! $, když
- $ \alpha\leq\frac{p(T_{\mbox{levý}(v)})}{p(T_v)}\leq 1-\alpha\,\! $
pro $ T_v\,\! $ jako podstrom určený (každým) vrcholem $ v\,\! $. O BB-$ \alpha\,\! $ stromech platí, že:
- výška$ (T)\leq 1+\frac{\log(n+1)-1}{\log{\frac{1}{1-\alpha}}}\,\! $
Takže jsou také vyvážené a operace mají zaručenou logaritmickou hloubku, vyvažuje se na nich také rotacemi a dvojrotacemi. Vždy totiž existuje $ \alpha\leq d\leq1-\alpha\,\! $ takové, že když mám strom, jehož oba podstromy splňují vlastnosti a navíc $ p(T_l)/p(T)\leq \alpha\,\! $ a $ p(T_l)/p(T)-1\,\! $ nebo $ p(T_l)+1/p(T)+1\,\! $ vyhovuje, vezmu $ \rho=\frac{p(T')}{p(T_r)}\,\! $, kde $ T'\,\! $ je určen levým synem $ T_r\,\! $, a pro $ \rho\leq d\,\! $ provedu ROTACE($ T\,\! $, $ T_r\,\! $), jinak DVOJROTACE($ T\,\! $, $ T_r\,\! $, $ T'\,\! $) a dostanu BB-$ \alpha\,\! $ strom (bez důkazu). Opačný případ je popsaný symetricky.
Mají pěknou vlastnost, kvůli které se používaly: pro $ \forall \alpha\,\! $ existuje $ c>0\,\! $ takové, že každá posloupnost $ k\,\! $ operací INSERT a DELETE volá max. $ c\cdot k\,\! $ rotací a dvojrotací.
B-Stromy a jejich varianty
(a,b)-stromy
$ (a,b)\,\! $-strom pro $ a\leq b\,\! $ přirozená je strom $ T\,\; $, který splňuje následující podmínky:
- každý vnitřní vrchol $ v\,\! $ stromu $ T\,\! $ různý od kořene $ t\,\! $ má alespoň $ a\,\! $ a nejvíc $ b\,\! $ synů
- všechny cesty od kořene k listům mají stejnou délku
Tato definice je ale pro praktické účely příliš obecná -- budeme chtít navíc podmínky:
- $ a\geq 2\,\! $ a $ b\geq 2a-1\,\! $
- kořen je buď list nebo má alespoň 2 a nejvíc $ b\,\! $ synů
Takový $ (a,b)\,\! $-strom existuje pro každý přirozený počet listů, jeho výška je mezi $ \log_b n\,\! $ a $ 1+\log_a(\frac{n}{2})\,\! $, tedy $ O(\log n)\,\! $. Indukcí: strom o výšce $ h\,\! $ má $ 2a^{h-1}\leq n\leq b^h\,\! $ listů (přidáním $ h\,\! $-té hladiny do stromu s $ k\,\! $ listy dostaneme strom s $ ka\leq n\leq kb\,\! $ listy.
Reprezentace množiny
Strom reprezentuje nějakou množinu $ S\,\! $ (prvků z univerza $ U\,\! $), když mám bijekci mezi uspořádáním $ S\,\! $ a lexikografickým uspořádáním listů.
Každý vnitřní vrchol $ v\,\! $ obsahuje informaci o počtu synů $ \rho(v)\,\! $, pole ukazatelů na syny $ S_v\,\! $ a pole $ H_v\,\! $ prvků z $ U\,\! $ takových, že $ i\,\! $-tý je největší v $ S\,\! $ reprezentovaný v podstromě $ i\,\! $-tého syna. Listy mají jen svůj prvek.
Pro každý prvek kromě největšího existuje vnitřní vrchol, který obsahuje jeho klíč, proto lze listy i vynechat a ukládat data ve vnitřních vrcholech (což ale není moc přehledné). Vrcholy můžou mít i odkaz na otce, nebo si otce můžu pamatovat při průchodech dolů (na vrcholech, ke kterým jsem nedošel od kořene, otce nepotřebuju).
Algoritmy
Máme pomocnou funkci VYHLEDEJ, který do hloubky projde stromem a vrátí nejbližší větší k nějakému prvku (nebo prvek sám, je-li ve stromě). Základní operace:
- MEMBER: přímo použije onu pomocnou operaci a pak zjistí, jestli našel, co hledal
- INSERT: vyhledám místo kam, pokud tam prvek není, vytvořím nový list, připojím na správné místo do $ S_v\,\! $ a postupně nahoru štěpím, je-li potřeba, extrémně rozštěpím kořen.
- DELETE: najdu prvek, najdu, kam je pověšený a to jedno políčko v $ S_v\,\! $ a $ H_v\,\! $ zruším, opravím $ \rho\,\! $, pokud dostanu méně než $ a\,\! $ synů v uzlu, spojím s bezprostředním bratrem (má-li ten právě $ a\,\! $ synů), nebo přesunu nějaký list z bratra do mého uzlu.
Oba algoritmy pracují v $ O(\log |S|)\,\! $ v nejhorším případě.
JOIN (bez prvku navíc): Přepokládá $ \max S_1<\min S_2\,\! $. Je-li $ h(T_1)\geq h(T_2)\,\! $, najde v $ T_1\,\! $ hladinu o 1 nad připojení a v ní největší prvek / vytvoří nadkořen $ T_1\,\! $ v případě rovnosti, slije do něj prvky obou kořenů a případně provede štěpení. Jinak hledá a připojuje v $ T_2\,\! $. Potřebuje čas $ O(|h(T_1)-h(T_2)|)\,\! $.
SPLIT: Prochází postupně dolů, rozděluje uzly (podstromy s prvky $ <x\,\! $, resp. $ \geq x\,\! $) a hází výsledky do 2 zásobníků. Pokud oddělí více než 1 krajní prvek, hodí na zásobník strom, jehož kořen je právě oddělená část uzlu, jinak na zásobník dává podstrom onoho krajního prvku. Tak pokračuje až k listům, pokud tam najde přímo $ x\,\! $, tak ho vyhodí. Stromy ze zásobníků spojí postupným voláním JOIN -- v 1 zásobníku jsou max. 2 stromy stejné výšky, celkem jich je $ k\leq 2\log_a |S|\,\! $ a jejich zpracování trvá $ O(\sum_{i=1}^{k-1}(h(T_i)-h(T_{i+1})+1))=O(h(T_1)+k)\,\! $.
ORD: S takovouto reprezentací efektivně nejde, proto musíme navíc $ \forall\,\! $ uzel udržovat pole $ P_v\,\! $ s počty vrcholů v jeho jednotlivých podstromech a při vkládání a odebírání ho průběžně aktualizovat. Pak v ORD procházím do hloubky a postupně přičítám velikosti přeskočených podstromů (pokud bych se přičtením dalšího dostal k $ 0\,\! $, jdu na nižší hladinu).
Implementace
- Pro vnitřní paměť se doporučuje $ a=2-3\,\! $ a $ b=2a\,\! $, pro vnější $ a\approx 100\,\! $ a $ b=2a\,\! $ (tj. v obou případech vlastně B-stromy).
- Při přístupu více uživatelů ke struktuře je problém s aktualizačními operacemi -- zamykání celého stromu není efektivní: použije se vyvažování shora dolů: algoritmus INSERT zamkne uzel, jeho otce a syny. Pak pokud je počet synů $ =b\,\! $, rozštěpí ho (předem), nebude se pak už štěpit zpátky.
- Aby tohle fungovalo (abych měl $ \geq a\,\! $ synů všude), je nutné $ b\geq 2a\,\! $.
- Podobně funguje DELETE -- najde-li uzel s $ a\,\! $ syny, provede "preventivně" slití nebo přesun.
- Provádí se tak víc slití a štěpení než v původní variantě, ale asymptoticky je to furt stejné.
- Pro takovéto struktury na externí paměti se doporučuje $ a\approx 100\,\! $ a $ b=2a+2\,\! $.
B-Stromy
B-strom řádu $ m\,\! $ je vlastně $ (a,b)\,\! $ strom pro $ a = \frac{m}{2}\,\! $ a $ b = m\,\; $. V určitých implementacích se ovšem data nacházejí už ve vnitřních vrcholech, potom má každý uzel vždy o 1 méně datových záznamů než potomků. Pokud jsou data uložena až v listech, jedná se o Redundantní B-strom.
Implementační detaily:
- Někdy jdou z uzlů na data jen pointery, listy můžou mít jinou (jednodušší) dat. strukturu než vnitřní uzly.
- Pro implementaci je vhodné pamatovat si celou aktuálně procházenou větev v nějakém bufferu.
- V redundantních stromech nemusím při odstranění dat odstraňovat klíč ve vnitrnich uzlech (lze podle toho hledat i kdyz to tam neni).
- Vylepšení -- vyvažování stránek-- při přetečení stránky se nejdřív dívám, jestli není volno v sousedních. Pokud ano, přerozdělím a upravím klíče -- zaručuje lepší zaplnění, ale je pomalejší. Podobně je možné vyvažovat počty se sousedy v případě vyhazování (i když nemerguju).
Další varianty
B* stromy -- Na základě vyvažování stránek zpřísníme podmínky na počet uzlů: Kořen ma min. 2 potomky, ost. uzly minimálně $ \lceil(2m-1)/3\rceil\,\! $ potomků, všechny větve jsou stejné dlouhé. Štěpení se odkládá, dokud nejsou sourozenci plní, potom se štěpí buď 2 do 3 (jen s jedním sourozencem), nebo 3 do 4 (s oběma) uzlů. Při odebírání se slévají 3 uzly do 2 (nebo 4 do 3). Štěpení a slévání jde zesložitit ještě na víc stránek.
Odložené štěpení -- používá stránku přetečení, vkládá znova, až když se naplní. Stránka přetečení může být jedna pro jeden listový uzel, nebo ji může sdílet nějaká skupina listů -- štěpí se, až když jsou všechny listy i přetečení zaplněné. Tedy pokud má strom víc než 1 úroveň, má všechny listy zaplněné (za předpokladu nepoužití DELETE). S odebíráním musím i slévat a štěpit skupiny -- jejich velikost není pevná.
Prefixové stromy -- pro redundantní B-stromy; klíče jsou co nejkratší řetězce nutné k odlišení listů, nikoliv celé hodnoty, které se nacházejí až v listech. Při vkládání a štěpení stránek se nějakou heuristikou hledá nejkratší prefix, který by dvě vznikající stránky oddělil. Mazaní a slévání -- žádná změna. Další zkrácení -- u potomků se neopakuje předpona klíče, kterou ma rodič -- to ale hodně zvýší nároky na CPU.
B+ stromy -- pro intervalové dotazy: zrychlení tím, že zřetězíme vždy uzly v jedné hladině (a nebo jenom listy), tj. přidáme do uzlů ukazatele na levého a pravého souseda.
Hladinově propojené (a,b)-stromy s prstem (Finger trees) -- pro vyhledávání navíc ještě přidáme odkaz na otce do každého uzlu a pro celou strukturu jeden "prst" -- odkaz na nějaký list. Vyhledávání začíná od prstu a postupuje nahoru, dokud nenajde podstrom, v němž by měl být hledaný prvek; potom se spustí dolů. Pokud je prvek poblíž prstu, je to rychlejší než klasická varianta. Typicky máme funkci nastevní prstu na nějaký prvek a pokud se motáme v jeho okolí, vyjde to lépe.
Proměnná délka zaznamů -- modifikace pro záznamy různé délky: neštěpit podle počtu záznamů, ale na zhruba 1/2 podle velikosti. Podmínka existence uzlu: součet délek záznamů v něm je $ \geq B/2\,\! $ kde $ B\,\! $ je délka uzlu(stránky) (pro B* stromy $ 2B/3\,\! $). Problémy: dlouhé klíče mají tendenci propadávat ke kořeni, tím se zmenšuje arita stromu; může se 1 stránka štěpit i na 3 (pokud vkládám záznam delší nez 1/2 stránky); vložením záznamu může dojít ke zmenšení stromu (jak, to se ve skriptech nepíše :( ) Nejde vyrobit nezávislé INSERT a DELETE, řešení: univerzální alg. nahrazování řetězce řetězcem, INSERT a DELETE jsou jeho spec. příp. Řešeni snižování arity stromu: minimalizace délky klíčů (nalezeni klíče min. délky, která navíc splňuje min. naplněni) - pro B* stromy docela složité.
Amortizované odhady počtů štěpení a slití a vyvážení
Důkaz je podle knihy K. Mehlhorn: Algorithms and Data Structures - The Basic Toolbox (Springer 2008). -- Tuetschek 20:35, 1 Sep 2010 (CEST)
Obecně může INSERT volat až $ \log(|S|)\,\! $-krát štěpení a DELETE $ \log(|S|)\,\! $-krát slití a jedno vyvážení (přesun). Začínáme-li s prázdným stromem a měříme na nějaké posloupnosti $ n $ operací, zjistíme, že jde amortizovaně o $ O(1)\,\! $.
Důkaz pro $ (2,4) $-stromy:
- Použijeme bankovní metodu, kdy INSERT bude stát dvě jednotky a DELETE jednu.
- Za štěpení a slití pak budeme platit vždy jednu jednotku, vyvážení nebude stát nic, protože je v každém DELETE voláno max. jednou a asymptoticky nic nezkazí.
- V jednotlivých uzlech stromu budeme udržovat následující počty jednotek podle stupně uzlů (přidáváme i stupně 1 a 5, které mají uzly těsně před štěpením a sléváním):
| $ \rho(v) $ | 1 | 2 | 3 | 4 | 5 |
| jednotek | 2 | 1 | 0 | 2 | 4 |
- Potom INSERT a DELETE bez štěpení díky své ceně udržují (občas i přeplácí) správné stavy jednotek v uzlech -- snížení stupně stojí max. 1 a zvýšení max. 2 jednotky.
- Dojde-li ke štěpení uzlu stupně 5 do uzlů stupňů 3 a 2, čtyři jednotky se zaplatí: jedna za rozdělení, jedna na účet nového uzlu stupně 2 a (max.) dvě za zvýšení stupně rodiče.
- Dojde-li k vyvažování (přesunu), máme 2 jednotky, což nám stačí k vytvoření dvou uzlů stupně 2 ze stupňů 1 a 3 a přebývá nám při vyvážení uzlů stupňů 1 a 4.
- Sléváme-li uzly stupně 1 a 2, máme 3 jednotky celkem: jednou zaplatíme vlastní slití, jednou snížení stupně rodiče a jedna zbyde.
Protože všechny možnosti zachovávají invariant, je vidět, že celkem bude max. $ 2n $ operací slití a štěpení. Důkaz (prý) jde rozšířit i na libovolné $ a $ a $ b\geq 2a $ (podle mě by mělo stačit zachovat ceny za operace a počty jednotek v krajních případech).
Pro $ b=2a-1\,\! $ lze bohužel jednoduše nalézt takové posloupnosti operací, kde počet slití a štěpení je $ O(n\log n)\,\! $, to samé, máme-li paralelní operace při $ b=2a+1\,\! $. Proto se doporučuje $ 2a\,\! $, resp. $ 2a+2\,\! $.
V hladinově propojeném stromě platí, že posloupnost $ n\,\! $ operací MEMBER, INSERT, DELETE a PRST vyžaduje $ O(\log n+\,\! $ čas na vyhledání prvků $ )\,\! $.
Trie
Sekce o Trie je popsaná podle Koubkových skript, skript Vidner-Kotal a knihy K. Mehlhorna -- Tuetschek 10:43, 22 Aug 2010 (CEST)
Trie je vlastně stromová reprezentace slovníku. Její označení zřejmě pochází od slova "retrieval". Jejím úkolem je reprezentovat množinu $ S\subseteq U\,\! $, kde $ U\,\! $ je tvořeno všemy slovy nad abecedou $ \Sigma, |\Sigma|=k\,\! $ o délce $ l\,\! $. Na této množině budeme provádět operace MEMBER, INSERT a DELETE.
Požadavek na délku se použije pouze u odhadů na složitost algoritmů. Ve skutečnosti ale není omezující -- slova můžeme vždycky doplnit nějakými znaky mezery nebo lehce algoritmy upravit, aby s kratšími slovy počítaly.
Základní varianta
Definice
Trie je strom takový, že každý vnitřní vrchol má $ k\,\! $ synů, odpovídajících všem znakům abecedy. Každému vrcholu lze rekurzivně přiřadit slovo nad abecedou $ \Sigma\,\! $ následujícím způsobem:
- Kořeni patří prázdné slovo $ \lambda\,\! $.
- $ a\,\! $-tému synu patří slovo otce doplněné o $ a\,\! $ (kde $ a\,\! $ je libovolné písmeno).
Pro každý vnitřní vrchol trie musí platit, že tento vrchol je prefixem nějakého slova z reprezentované množiny $ S\,\! $. Každý list obsahuje jeden bit, který udává přítomnost nebo nepřítomnost slova, které představuje, v množině $ S\,\! $.
Je vidět, že taková struktura je dost paměťově náročná -- každý vrchol potřebuje paměť $ O(k)\,\! $ a celkem máme aspoň tolik vrcholů, co bodů množiny, násobeno délkou cesty k nim, tedy $ O(kl|S|)\,\! $.
Operace
MEMBER je velice jednoduchý -- postupně sestupuje stromem podél syna, který odpovídá $ i\,\! $-tému písmenu hledaného slova v $ i\,\! $-tém kroku. Pokud se dostane do listu dřív než dojde na konec slova, skončí neúspěchem. Jinak vrátí informaci o přítomnosti slova z listu, do kterého se dostal.
INSERT dojde do listu podobně jako MEMBER. Potom (je-li to potřeba) mění listy na vnitřní vrcholy a vkládá pokračování cesty až do dosažení délky slova. V posledním kroku upraví indikaci v listu.
DELETE vyhledá prvek a nastaví indikaci v jeho listu na FALSE. Pak se postupně vrací a dokud nalézá jen samé listy s FALSE, zruší celý vrchol a změní ho na list s FALSE.
Algoritmus MEMBER projde až $ l\,\! $ vrcholů a každý v konstantním čase (vrcholy se indexují přímo písmeny abecedy), tedy je $ O(l)\,\! $. Algoritmy INSERT a DELETE vyžadují čas $ O(kl)\,\! $, protože úprava jednoho vrcholu vyžaduje až $ k\,\! $ operací.
Komprimované Trie
Trie upravíme tak, že vyházíme vrcholy, jejichž slovo je prefixem stejné množiny slov jako slovo jejich otců (tj. vrcholy, kde nedochází k žádnému větvení a je jen jedna možnost pokračování). Ve vrcholech si teď ale místo toho musíme udržovat informaci o aktuální hloubce $ \kappa(v)\,\! $ a navíc v listech musíme držet celé slovo, které reprezentují (abychom neztratili písmena z vrcholů, které jsme vyházeli).
Operace pak bude třeba upravit, ale protože takto upravené trie má jen $ S-1\,\! $ vnitřních vrcholů, paměťová náročnost klesla na $ O(k|S|)\,\! $
Operace
MEMBER pracuje podobně, ale ve vrcholu $ v\,\! $ vždy testuje $ \kappa(v) + 1\,\! $-ní písmeno hledaného slova. Nakonec (protože neotestoval všechna písmena a mohlo by tedy dojít ke kolizi) navíc porovná slovo uložené ve vrcholu se slovem, které jsme hledali.
INSERT pro nějaké slovo $ x\,\! $ opět vyhledá místo pro vložení a dojde do listu, kde najde jiné slovo $ y\,\! $. Pak vezme největší společný prefix slov $ x,y\,\! $ a v jeho místě strom rozdělí -- pokud ve správné hloubce už je vnitřní vrchol, pokračuje z něj, jinak nový dělící vrchol přidá. Potom upraví hodnoty v listech.
DELETE zruší informaci o mazaném slově stejně jako předtím. Navíc ale pokud zjistí, že otec "vyčištěného" listu v hierarchii stromu má jen jednoho dalšího potomka -- vnitřní uzel, nacpe tohoto potomka na jeho místo.
Je vidět, že INSERT a DELETE změní maximálně jeden vnitřní vrchol a pracují tak v $ O(k+l)\,\! $.
Očekávaná hloubka
Odhady časů pro operace MEMBER, INSERT a DELETE závisí na (maximální) délce slov $ l\,\! $, ale takové hloubky komprimované trie dosáhne jen v nejhorším případě. Chceme proto odhad očekávané hloubky, za předpokladu, že reprezentovaná množina $ S\,\! $ je vzorkem dat z rovnoměrného rozdělení (což bývá často přibližně splněno).
Označíme $ q_d\,\! $ pravděpodobnost, že komprimovaný trie nad množinou $ S, |S| = n\,\! $ má hloubku aspoň $ d_n = d\,\! $. Pak je naše očekávaná (střední) hodnota hloubky:
- $ E(d_n) = \sum_{i=1}^{\infty} i(q_i - q_{i+1}) = \sum_{i=1}^{\infty} q_i\,\! $
Odhadneme proto velikost $ q_d\,\! $. Víme, že hloubka trie je menší než $ d\,\! $, když prefixy o délce $ d\,\! $ slov z naší množiny rozlišují tato slova jednoznačně. Pravděpodobnost, že toto nastane, je (počet jednoznačných prefixů a k nim počet libovolných doplnění do délky $ l\,\! $, děleno počtem jednoznačných slov délky $ l\,\! $, vše nad abecedou o velikosti $ k\,\! $):
- $ P( $jednoznačné rozlišení o délce $ d\,\! $) $ = \frac{\mathbf{}\binom{k^d}{n}k^{n(l-d)}}{\binom{k^l}{n}}\,\! $
Z toho:
- $ q_d \leq 1 - P( $jednoznačné rozlišení o délce $ d-1) = $ $ 1 - \frac{\mathbf{}\binom{k^{(d-1)}}{n}k^{n(l-d+1)}}{\binom{k^l}{n}} \leq 1 - \frac{\left(\prod_{i=0}^{n-1}(k^{d-1}-i)\right)k^{n(l-d+1)}}{k^{nl}} = 1 - \prod_{i=0}^{n-1}\left(1 - \frac{i}{k^{d-1}}\right) \leq 1 - \exp\left(\frac{-n^2}{k^{d-1}}\right) \leq \frac{n^2}{k^{d-1}} $
Poslední kroky jsme mohli udělat, protože platí (integrál s nerovností můžeme použít, protože daný logaritmus je klesající, při výpočtu integrálu použijeme substituci za $ 1-\frac{x}{k^{d-1}}\,\! $):
- $ \prod_{i=0}^{n-1}\left(1 - \frac{i}{k^{d-1}}\right) = \exp\left(\sum_{i=0}^{n-1}\ln\left(1-\frac{i}{k^{d-1}}\right)\right) \geq $ $ \geq \exp\left(\int_{0}^{n}\ln\left(1-\frac{x}{k^{d-1}}\right) \mathrm{d} x\right) = \exp\left((n-k^{d-1})\ln\left(1-\frac{n}{k^{d-i}}\right) - n\right) \leq \exp\left(\frac{-n^2}{k^{d-1}}\right)\,\! $
Očekávaná výška stromu pak vyjde, položíme-li $ c = 2\lceil \log_k n\rceil\,\! $:
- $ \sum_{i=1}^{\infty} q_i = \sum_{i=1}^c q_i + \sum_{i=c+1}^{\infty} q_i \leq \sum_{i=1}^{c} 1 + \sum_{i=c+1}^{\infty} \frac{n^2}{k^{i-1}} = c + \frac{n^2}{k^c}\left(\sum_{i=0}^{\infty}\frac{1}{k^i}\right) \leq 2\lceil \log_k n \rceil + \frac{1}{1-\frac{1}{k}}\,\! $
Trie v tabulce
Pokud se vzdáme operací INSERT a DELETE, můžeme trie reprezentovat na extrémně zcvrklém prostoru. Nejdříve si ho představme jako matici $ M\,\! $ dimenze $ r\times s\,\! $, kde každý vnitřní vrchol odpovídá jednomu řádku a sloupce jsou písmena abecedy. Potom na pozici $ M(v,a)\,\! $ je $ a\,\! $-tý syn vrcholu $ v\,\! $. Pole matice může obsahovat buď odkazy na další vrcholy (identifikátor řádku), nebo přímo slova, která jsou obsažena v reprezentované množině, nebo prázdnou hodnotu null. Ve vedlejším poli si musíme uchovat i hloubky vrcholů odpovídající nekomprimovanému trie -- $ \kappa(v)\,\! $.
Komprese matic -- uložení do pole
Hodnoty null ale nepřinášejí novou informaci -- stačí při průchodu maticí na další vrcholy testovat, zda nám stoupá hodnota $ \kappa(v)\,\! $ a nakonec provést test shody s nalezeným prvkem. Díky tomu můžeme na místa, kde je null, v klidu ukládat něco jiného.
Matici $ M\,\! $ tak můžeme reprezentovat dvěma poli
- $ VAL\,\! $ -- v něm budou hodnoty z různých řádků matice
- $ RD\,\! $ ("row displacement", "posunutí řádku") -- bude udávat, kde začíná který řádek původní matice $ M\,\! $ ve $ VAL\,\! $
Jednotlivé datové řádky původní matice se v poli $ VAL\,\! $ v klidu můžou překrývat, pokud překryté hodnoty jsou jen null. Formálně musíme zachovat, že když $ M(i,j)\,\! $ je definováno, pak $ M(i,j) = VAL(RD(i) + j)\,\! $ a že když $ M(i,j)\,\! $ a $ M(i',j')\,\! $ jsou definovány pro $ (i,j)\neq (i',j')\,\! $ , pak $ RD(i) + j \neq RD(i') + j'\,\! $.
Pro nalezení "dobrého" rozložení řádků původní matice do pole $ VAL\,\! $ se používá algoritmus First-Fit Decreasing:
- Pro každý řádek původní matice $ M\,\! $ spočteme, kolik míst je non-null a setřídíme řádky matice podle této hodnoty v klesajícím pořadí
- Bereme řádky podle setřídění a vkládáme je na první místo od začátku pole $ VAL\,\! $ tak, že neporušují výše uvedené podmínky.
Označíme počet všech non-null hodnot jako $ m\,\! $ a počet non-null hodnot v řádcích s alespoň $ l\,\! $ non-null hodnotami jako $ m_l\,\! $. Pokud řádky matice $ M\,\! $ splňují pravidlo harmonického rozpadu, tj. $ \forall l: m_l\leq \frac{m}{l+1}\,\! $ (tj. např. více než polovina řádků obsahuje jen jednu skutečnou hodnotu), pak pro každý řádek $ i\,\! $ platí $ RD(i)<m\,\! $ a algoritmus stavby polí potřebuje $ O(rs+m^2)\,\! $ času (důkaz je hnusný).
Posouvání sloupců
Protože podmínku harmonického rozpadu splňuje jen málo matic, upravíme si obecné matice tak, aby ji splňovaly taky. Využijeme toho, že matici trochu "natáhneme" do počtu řádků (tím se, pravda, zvětší pole $ RD\,\! $) a jednotlivé sloupce v ní rozstrkáme tak, aby v jednom řádku nevyšlo moc zaplněných míst najednou. Kde začíná který sloupec si zapamatujeme v dalším pomocném poli $ CD\,\! $ ("column displacement", "posunutí sloupce").
"Dobré" posunutí sloupců nalezneme obyčejným přístupem First-Fit, když pro každý sloupec $ j\,\! $ nalezneme nejmenší číslo $ CD(j)\,\! $ splňující:
- $ m(j+1)_l\leq \frac{m}{f(l,m(j+1))}\ \forall l = 0,1,\dots\,\! $
Hodnota $ m(j)\,\! $ je počet všech zaplněných míst v prvních $ j\,\! $ sloupcích právě konstruované matice a $ m(j)_l\,\! $ je počet zaplněných míst v řádcích s alespoň $ l\,\! $ zaplněnými místy.
Pozorování:
- Je vidět, že každá funkce $ f\,\! $ musí splňovat $ f(0,m(j))\leq \frac{m}{m(j)}\ \forall j\,\! $, protože jinak by v algoritmu nemohla být splněna testovaná podmínka pro $ l=0\,\! $ (protože $ m_j = m(j)_0\,\! $).
- Dále musí funkce $ f\,\! $ splňovat nerovnost $ f(l,m)\leq l+1\ \forall l\,\! $, aby výsledná matice splňovala podmínku harmonického rozpadu.
Dá se ukázat (a je to hnusný důkaz), že vhodná funkce je třeba $ f(x,y) = 2^{x(2-\frac{y}{m})}\,\! $, protože splňuje obě podmínky a navíc výsledný vektor $ CD\,\! $ má délku $ s\,\! $, vektor $ RD\,\! $ má délku menší než $ 4m\log\log m + 15.3m + r\,\! $ a vektor $ VAL\,\! $ má délku menší než $ m+s\,\! $. Protože hodnoty $ CD\,\! $ indexují $ RD\,\! $ a hodnoty $ RD\,\! $ indexují $ VAL\,\! $, plynou z toho omezení i na hodnoty v nich uložené.
Čas celého algoritmu vytváření matic je $ O(s(r+m\log\log m)^2)\,\! $.
Další komprese vektoru RD
Protože $ M\,\! $ má jen $ m\,\! $ definovaných mít, z algoritmu pro výpočet $ RD\,\! $ plyne, že jen max. $ m\,\! $ míst v tomto vektoru bude různých od nuly. Proto můžeme použít následující kompresi (řekněme, že nenulových míst je $ t\,\! $):
- Vektor $ RD\,\! $ rozdělíme na $ n\,\! $ bloků o délce $ d\,\! $.
- Vytvoříme nový vektor $ CRD\,\! $ o délce $ t\,\! $, který obsahuje jen nenulové prvky původního vektoru. Označme jejich původní pozice $ i_j, j = 0\dots t-1\,\! $ a jejich pozice ve vektoru $ CRD\,\! $ jako $ v(i_j)\,\! $.
- Vytvoříme vektor $ BASE\,\! $ o délce $ n\,\! $, kde $ BASE(x) = \begin{cases}-1 & i_j \div d \neq x\ \forall j = 0,\dots t-1 \\ \min\{l; i_l\div d = x\} & \mbox{jinak}\end{cases}\,\! $1
- Vytvoříme matici $ OFFSET\,\! $ typu $ n\times d\,\! $, kde $ OFFSET(x,y) = \begin{cases} -1 & x\cdot d + y \neq i_j\ \forall j \\ j - BASE(x) & x\cdot d + y = i_j \end{cases}\,\! $
- Uložíme matici $ OFFSET\,\! $ do vektoru $ OFF\,\! $ dimenze $ n\,\! $ tak, že z každého řádku vytvoříme číslo v soustavě o základu $ d+1\,\! $: $ OFF(x) = \sum_{k=0}^{d-1}(OFFSET(x,k)+1)(d+1)^{k}\,\! $.
Potom platí, že:
- $ v(h) = 0 \Leftrightarrow OFFSET(h\div d, h\mod d) = -1\,\! $
- $ v(h) = 1 \Rightarrow h = BASE(h\div d) + OFFSET(h\div d, h\mod d)\,\! $
- $ OFFSET(i,j) = ((OFF(i)\div (d+1)^j)\mod (d+1)) -1\,\! $
Celá tahle legrace má smysl, jen pokud $ d\ll n,\; $ a $ t<n\,\! $. Když $ d\leq \lceil \log\log n\rceil\,\! $, pak lze celé trie uložit pomocí pěti vektorů dimenze $ n\,\! $ s hodnotami menšími než $ 4n\log\log n\,\! $.
* ^ ad 1 Funkce $ \div\,\! $ tu označuje celočíselné dělení (podobné operaci div z Pascalu).
Haldy
Haldy se používají pro měnící se uspořádané množiny. Nevyžaduje se efektivní operace MEMBER (často se předpokládá s argumentem operace informace o uložení prvku). Požadují se malé nároky na paměť a rychlost ostatních operací.
Definice, operace
Halda je stromová struktura nad množinou (dat) $ S\,\! $, jejíž uspořádání je dáno funkcí $ f:S\to \mathbb{R}\,\! $, splňující lokální podmínku haldy:
- $ \forall v\in S: f(\,\! $otec$ (v))\leq f(v)\,\! $, případně v duální podobě.
Množina je reprezentovaná haldou, když přiřazení prvků vrcholům haldy je bijekce, splňující podmínku haldy. Různé druhy hald se liší podle dalších podmínek, které musí splňovat stromové struktury.
- Krom běžných operací můžu měnit uspořádání: operace INCREASE a DECREASE změní velikost $ f\,\! $ na nějakém daném prvku $ s\,\! $ se známým uložením o $ +a\,\! $, $ -a\,\! $.
- Další operace: DELETEMIN -- smazání prvku s nejmenší hodnotou $ f\,\! $.
- Pro operaci DELETE budeme požadovat přímé zadání uložení prvku.
- Navíc definujeme operaci MAKEHEAP -- vytvoření haldy při známé množině a $ f\,\! $,
- a MERGE -- slití dvou hald do jedné, reprezentující $ S_1 \cup S_2\,\! $ a $ f_1\cup f_2\,\! $, aniž by se ověřovala disjunktnost.
Regulární haldy
Pro $ d\,\! $-regulární strom ($ d\in\mathbb{N}\,\! $) s kořenem $ r\,\! $ platí, že existuje pořadí synů vnitřních vrcholů takové, že očíslování prohledáváním z $ r\,\! $ do šířky splňuje:
- každý vrchol má nejvýše $ d\,\! $ synů
- když vrchol není list, tak všechny vrcholy s menším číslem mají právě $ d\,\! $ synů
- má-li vrchol méně než $ d\,\! $ synů, pak všechny vrcholy s většími čísly jsou listy
Potom takový strom s $ n\,\! $ vrcholy má max. jeden ne-list, který nemá právě $ d\,\! $ synů, jeho výška je $ \lceil\log_d(n(d-1)+1)\rceil\,\! $. Čísla synů vrcholu s číslem $ k\,\! $ jsou $ (k-1)d+2,\dots,kd+1\,\! $, číslo otce je $ 1+\lfloor\frac{k-2}{d}\rfloor\,\! $. Takto vytvořená halda umožňuje i efektivní reprezentaci v poli.
Operace na regulárních haldách
- Není známa efektivní operace MERGE.
- Máme pomocné operace UP, DOWN, posunující prvek níž/výš ve struktuře, dokud není splněna podmínka haldy ("probublávání").
- INSERT jen vloží nový prvek za poslední a spustí UP
- DELETE nahradí odstraněný prvek posledním listem a volá UP nebo DOWN podle potřeby
- DELETEMIN odstraní kořen, nahradí ho posl. listem a volá DOWN
- MIN jen vrátí kořen
- INCREASE a DECREASE změní hodnotu $ f\,\! $ nějakého prvku a zavolají DOWN, resp. UP (pozor, je to naopak, než názvy napovídají).
- Operace MAKEHEAP vytvoří libovolný strom a pak postupně od posledního ne-listu ke kořeni volá na všechno DOWN.
U všech operací je korektnost zajištěna podmínkou haldy (a tím, že UP a DOWN zaručí její splnění).
Složitost operací
Běh DOWN vyžaduje $ O(d)\,\! $ a UP $ O(1)\,\! $ v každém cyklu, takže celkem jde o $ O(d\log|S|)\,\! $ a $ O(\log|S|)\,\! $.
Haldu lze vytvořit opakovaným INSERTem v čase $ |S|\log|S|\,\! $, ale pro větší množiny je rychlejší MAKEHEAP -- uvažujeme-li, že operace DOWN vyžaduje čas odpovídající výšce vrcholu. Ve výšce $ k-i\,\; $ je $ d^i\,\; $ vrcholů. Tím dostávám celkový čas $ O(\sum_{i=0}^{k-1}d^i(k-i)d)\,\! $, což se dá odhadnout jako $ O(d^2|S|)\,\! $.
Aplikace
Heapsort -- vytvoření haldy a postupné volání MIN a DELETEMIN. Lze ukázat, že pro $ d=3,d=4\,\! $ je výhodnější než $ d=2\,\! $, empiricky je do cca $ 1 000 000\,\! $ prvků $ d=6\,\! $ nebo $ d=7\,\! $ nejlepší. Pro delší posloupnosti je možné $ d\,\! $ zmenšit.
Dijkstra -- normální Dijkstrův algoritmus, jen vrcholy grafu uchovávám v haldě, tříděné podle aktuálního $ d\,\! $ (horního odhadu vzdálenosti). Složitost $ O((m+n)\log n)\,\! $, pro $ d=\max\{2,\frac{m}{n}\}\,\! $ je to $ O(m\log_d n)\,\! $ a pro husté grafy ($ m>n^{1+\varepsilon}\,\! $) je lineární v $ m\,\! $.
Leftist haldy
Leftist halda je binární strom ($ T,r\,\! $). Označme npl($ v\,\! $) délku nejkratší cesty z $ v\,\! $ do vrcholu s max. 1 synem. Leftist halda musí splňovat následující podmínky:
- má-li vrchol 1 syna, pak je vždy levý
- má-li 2 syny $ l,p\,\! $ , pak npl($ p\,\! $)$ \leq\,\! $npl($ l\,\! $)
- podmínka haldy na klíče prvků (ex. přiřazení prvků vrcholům stromu)
Pro leftist haldu se definuje pravá cesta (posl. pravých synů) a pokud máme takovou cestu délky $ k\,\! $ z vrcholu $ v\,\! $, víme, že podstrom $ v\,\! $ do hloubky $ k\,\! $ je úplný binární strom. Délka pravé cesty z každého vrcholu je tedy logaritmická ve velikosti podstromu.
Operace jsou založeny na algoritmech MERGE a DECREASE.
- MERGE testuje prázdnost jednoho ze stromů (a pokud je jeden prázdný, vrátí ten druhý jako výsledek). Pokud ne, volá se rekurzivně na podstrom pravého syna kořene s menším klíčem dohromady s celým druhým a výsledek připojí místo onoho pravého syna. Pokud neplatí podmínka na npl, syny vymění.
- INSERT je to samé co vytvoření jednoprvkové haldy a zavolání MERGE.
- DELETEMIN je zMERGEování synů kořene (a jeho zahození).
- MAKEHEAP je vytvoření hald z jednotl. prvků. Nacpu je do fronty a potom v cyklu vyberu dva první, zmerguju a hodím výsledek na konec, dokud mám ve frontě víc než 1 haldu.
INCREASE a DECREASE se dělají jinak.
- Mám pomocnou operaci OPRAV, která odtrhne podstrom a dopočítá všem vrcholům správné npl. Po odtržení vrcholu a příp. přehození pravého syna doleva jde nahoru, dokud provádí změny npl (možno až do kořene), vztahuje npl odspoda a příp. prohazuje syny.
- DECREASE se pak udělá snížením hodnoty ve vrcholu, zavoláním OPRAV, tj. jeho odříznutím od zbytku haldy, a MERGE podstromu a zbytku.
INCREASE: zapamatuju si levý a pravý podstrom vrcholu s mým prvkem a provedu na něj OPRAV (vyhodím ho), potom vyrobím nový vrchol s mým prvkem se zvednutou hodnotou a jako samostatnou haldu ho zMERGEuju s levým podstromem. Pravý podstrom zMERGEuju se zbytkem haldy a nakonec s tím zMERGEuju výsledek MERGE levého podstromu a zvednutého prvku.
Složitost
1 běh MERGE bez rekurze je $ O(1)\,\! $, hloubka rekurze je omezena pravými cestami, takže je to $ O(\log(|S_1|+|S_2|))\,\! $. Z toho plyne logaritmovost INSERT a DELETEMIN.
Pro MAKEHEAP se uvažuje, kolikrát projdou haldy frontou: po $ k\,\! $ projití frontou mají velikost $ 2^{k-1}\,\! $ a tedy fronta obsahuje $ \lceil\frac{|S|}{2^{k-1}}\rceil\,\! $ hald. Jeden MERGE je $ O(k) $ a jedno projití frontou pro všechny haldy tedy trvá $ O(k\lceil\frac{|S|}{2^{k-1}}\rceil)\,\! $. Celkem dostávám $ O(|S|\sum_{k=1}^{\infty}\frac{k}{2^{k-1}})=O(|S|)\,\! $ (součet řady je $ 4\,\! $).
OPRAV chodí jen po pravé cestě, takže má logaritmickou složitost. INSERT, INCREASE a DECREASE se díky ní dostanou taky na $ O(\log|S|)\,\! $, protože jejich části kromě MERGE a OPRAV mají konstantní složitost.
Binomiální haldy
Binomiální stromy se definují rekurentně jako $ H_i\,\! $, kde $ H_0\,\! $ je jednoprvkový a $ H_{i+1}\,\! $ vznikne z dvou $ H_i\,\! $, kdy se kořen jednoho stane dalším (krajním) synem kořenu druhého. Pak strom $ H_i\,\! $ má $ 2^i\,\! $ prvků, jeho kořen má $ i\,\! $ synů, jeho výška je $ i\,\! $ a podstromy určené syny kořene jsou právě $ H_{i-1},\dots,H_0\,\! $.
Binomiální halda reprezentující $ S\,\! $ je seznam stromů $ T_i\,\! $ takový, že celkový počet vrcholů v těchto stromech je $ |S|\,\! $ a je dáno jednoznačné přiřazení prvků vrcholům, respektující podmínku haldy. Každý strom je přitom izomorfní s nějakým $ H_i\,\! $ a dva $ T_i,T_j, i\neq j\,\! $ nejsou izomorfní.
Existence binomiální haldy pro každé přirozené $ |S|\,\! $ plyne z existence dvojkového zápisu čísla.
Operace
Operace na binomiálních haldách jsou založené na MERGE.
- MERGE pracuje stejně jako binární sčítání -- za pomoci operace SPOJ (slepení dvou stromů, přilepím jako syna toho, který má v kořeni vyšší klíč) slepí stromy stejného řádu, přenáší výsledky do dalšího spojování (přenos + obě haldy mající strom daného řádu = vyplivnutí 1 stromu na výsledek a spojení zbývajících dvou).
- INSERT je MERGE s jednoprvkovou haldou.
- MIN je projití kořenů a vypsání nejmenšího.
- DELETEMIN je MIN, odebrání stromu s nejmenším prvkem v kořeni a přidání (MERGE) podstromů jeho kořene do haldy.
- INCREASE a DECREASE se dělají úplně stejně jako u regulárních hald.
- Přímo není podporováno DELETE, jen jako DECREASE + DELETEMIN.
- MAKEHEAP se provádí opakováním INSERT.
Složitost MERGE je $ O(\log|S_1|+\log|S_2|)\,\! $, protože 1 krok SPOJ je konstantní. Halda má nejvýše $ \log|S|\,\! $ stromů, takže MIN a DELETEMIN mají tuto složitost. Výška všech stromů je $ \leq\log|S|\,\! $, což dává složitost INCREASE $ O(\log^2|S|)\,\! $ a DECREASE $ O(\log|S|)\,\! $. Pro odhad složitosti MAKEHEAP se použije amortizovaná složitost přičítání jedničky k binárnímu číslu, což je $ O(1)\,\! $, tedy celkem $ O(|S|)\,\! $.
Líná implementace
Vynecháme předpoklad neexistence dvou izomorfních stromů v haldě a budeme "vyvažování" provádět jen u operací MIN a DELETEMIN, kdy se stejně musí projít všechny stromy. MERGE je pak prosté slepení seznamů hald. Vyvažování se provádí operací VYVAZ, která sloučí izomorfní stromy (podobně jako MERGE z pilné implementace).
Složitost INSERT a MERGE je $ O(1)\,\! $, ale DELETEMIN a MIN v nejhorším případě $ O(|S|)\,\! $.
Amortizovaná složitost vychází ale líp: použijeme potenciálovou metodu, když za hodnocení konfigurace $ w(H)\,\; $ zvolíme počet stromů v haldě $ |\mathcal{H}|\,\! $. INSERT a MERGE ho nemění, resp. mění o $ 1\,\! $, takže jsou stále $ O(1)\,\! $.
Operace VYVAZ potřebuje $ O(|H|)\,\! $, protože slití dvou stromů trvá konstantně dlouho a nelze slévat víc stromů, než kolik jich je v haldě. Kromě operace VYVAZ potřebuje MIN $ O(|\mathcal{H}|)\,\! $ a DELETEMIN $ O(|\mathcal{H}|+\log|S|)\,\! $ (max. stupeň stromu je logaritmický).
Dohromady vychází amortizovaná složitost pro MIN: $ am(o) = t(o) - w(H) + w(H') = O(|\mathcal{H}|-|\mathcal{H}|+\log|S|)\,\! $, protože výsledný počet stromů $ |H'|\,\; $ odpovídá pilné implementaci. Pro DELETEMIN podobně dostanu $ O(|\mathcal{H}|+\log|S|-|\mathcal{H}|+\log|S|)=O(\log|S|)\,\! $.
Fibonacciho haldy
Definují se jako množiny stromů, které splňují podmínku haldy a musely vzniknout posloupností operací z prázdné haldy. Všechny operace zachovávají podmínku, že jednomu vrcholu lze odříznout max. dva syny. Strom má rank $ i\,\! $, má-li jeho kořen $ i\,\! $ synů (podobné jako izomorfismus s $ H_i\,\! $ u binomiálních hald).
Podmínka odříznutí max. dvou synů se zachovává pomocnou operací VYVAZ2. Když vrchol není kořen a byl mu předtím někdy odříznut syn, je speciálně označený. VYVAZ2 prochází od daného vrcholu ke kořeni a dokud nalézá označené vrcholy, odtrhává je i s jejich podstromy, ruší jejich označení a vkládá do haldy jako zvláštní stromy. Když se vrchol stane kořenem, označení se zapomene.
Operace
MERGE, INSERT, MIN a DELETEMIN jsou stejné jako v líné implementaci binomiálních hald, jen požadavek na isomorfismus s $ H_i\,\! $ je nahrazen požadavkem na daný rank. Pomocné operace z binomiálních hald VYVAZ a SPOJ jsou také stejné.
DECREASE, INCREASE a DELETE vycházejí z leftist hald. Používají pomocnou operaci VYVAZ2
- DECREASE odtrhne podstrom určený snižovaným vrcholem (není-li to už kořen), zruší u něj případné označení a vloží ho zvlášť do haldy, na odtržené místo zavolá VYVAZ2.
- INCREASE provede to samé, jen ještě roztrhá podstrom zvedaného vrcholu (odtrhne všechny syny, zruší jejich příp. označení a vloží jako samostatné stromy do haldy) a vloží zvednutý vrchol do haldy zvlášť.
- DELETE je to samé co INCREASE, bez přidání vrcholu zpět do haldy.
Korektnost a složitost
Operace SPOJ podobně jako u binomiálních hald vyrobí ze dvou stromů ranku $ i\,\! $ jeden strom ranku $ i+1\,\! $. Operace VYVAZ2 zajistí, že od každého vrcholu kromě kořenů byl odtržen max. 1 syn -- když odtrhnu dalšího, odtrhu i tento vrchol a propaguju operaci nahoru.
Složitost operací:
- MERGE a INSERT je $ O(1)\,\! $ (stejně jako u binomiálních hald)
- MIN má $ O(|\mathcal{H}|)\,\! $ (nemění označení vrcholů)
- DELETEMIN $ O(|\mathcal{H}|+\mathrm{maxrank}(\mathcal{H}))\,\! $, kde $ maxrank\,\! $ udává maximální rank stromu v haldě (může navíc odznačit některé vrcholy)
- DECREASE je $ O(1+c)\,\! $, kde $ c\,\! $ je počet odznačených vrcholů (navíc označí max. 1 vrchol)
- INCREASE a DELETE jsou $ O(1+c+d)\,\! $, kde navíc $ d\,\! $ je počet synů zvedaného nebo odstraňovaného vrcholu (také označí navíc max. 1 vrchol).
Pro výpočet amortizované složitosti použijeme potenciálovou metodu a zvolíme hodnotící funkci $ w\,\! $ jako počet stromů v haldě + $ 2\times\,\! $ počet označených vrcholů. Můžeme říct, že amortizovaná složitost MERGE, INSERT a DECREASE je $ O(1)\,\! $.
Označme max. rank stromů v lib. haldě reprezentující $ n\,\! $-prvkovou množinu jako $ \rho(n)\,\! $. Amortizovaná složitost MIN, DELETEMIN, INCREASE a DELETE pak je $ O(\rho(n))\,\! $ (pro MIN a DELETEMIN je vzorec amortizované složitosti podobný jako u binomiálních hald, pro INCREASE a DELETE je to vidět přímo ze vzorců).
Pro odhad $ \rho(n)\,\; $ je potřeba znát fakt, že $ i\,\! $-tý nejstarší syn libovolného vrcholu má aspoň $ i-2\,\! $ synů (plyne z toho, že se slévají jen stromy stejného řádu a odtrhnout lze max. jednoho syna).
Vezmeme tedy nejmenší strom $ T_j\,\; $ ranku $ j\,\; $, který toto splňuje. Ten musí být složením $ T_{j-1}\,\; $ a $ T_{j-2}\,\; $ (vzniká tak, že se slijí dva $ T_{j-1}\,\; $ a potom se na tom, který je pověšený jako syn nového kořenu, provede DECREASE a tím se z něj stane $ T_{j-2}\,\; $). Z minimálního počtu synů se dá odvodit i rekurence $ |T_k| \geq 1 + 1 + |T_0| + \dots + |T_{k-2}| $, která dá indukcí to samé.
Potom $ |T_{k+1}| = F_k $, kde $ F_k $ je $ k $-té Fibonacciho číslo. Pro Fibonacciho čísla platí, že $ \lim_{k\to\infty} F_k = \frac{1}{\sqrt{5}}\left(\frac{1 + \sqrt{5}}{2}\right)^k $. Proto je $ \rho(n) = O(\log(n))\,\; $, což dává logaritmickou amortizovanou složitost pro MIN, DELETEMIN, INCREASE a DELETE. Z toho pochází i název Fibonacciho haldy.
Aplikace
Fibonacciho haldy se díky své rychlosti INSERT, DECREASE a DELETEMIN často používají v grafových algoritmech. Praktické porovnání rychlosti s jinými haldami však není dosud přesně prostudováno.
Motivací pro vývoj Fibonacciho hald byla možnost aplikace v Dijkstrově algoritmu. Dává totiž složitost celého algoritmu $ O(m+ n\log n)\,\! $, což by mělo být lepší pro velké, ale řídké grafy proti $ d\,\! $-regulárním haldám. O prakticky zjištěném "zlomu" ale nevíme.
Státnice -- Matematická lingvistika
Složitost a vyčíslitelnost -- Tvorba algoritmů, Odhady složitosti, NP-úplnost, Aproximační algoritmy, Vyčíslitelné funkce, Rekurzivní množiny, Nerozhodnutelné problémy, Věty o rekurzi.
Datové struktury -- Stromy, Hašování, Dynamizace, Vnější paměť, Třídění.
Formální popis jazyka -- Závislostní syntax, Frázové gramatiky, Obecná lingvistika, FGD, Formální sémantika
Statistické metody -- Korpusy, Strojové učení, Stochastické metody, Experimenty
Automatické zpracování jazyka -- Analýza jazyka, Generování jazyka, Analýza a syntéza řeči, Extrakce informací, Strojový překlad