Řešené otázky NTIN090/Savitch Sandbox
Z ωικι.matfyz.cz
Věta ( počet konfigurací TS/NTS ): Nechť $ M $ je libovolný TS (DTS nebo NTS), který pracuje v prostoru $ f(n) $, pak existuje konstanta $ c_M $ (jejíž hodnota je závislá na stroji $ M $), pro kterou platí, že počet konfigurací $ M $ je nejvýš $ 2^{c_M f(n)} $.
- Dk
- Nechť $ M = (Q, Σ, δ, q_0, F ) $. Konfigurace se skládá ze slova na pásce, polohy hlavy v rámci tohoto slova a stavu, v němž se stroj $ M $ nachází. Délka slova na pásce je omezená $ f(n) $, počet různých poloh hlavy v rámci tohoto slova je $ f(n) $ a počet stavů je $ |Q| $. Počet konfigurací je tedy shora omezen pomocí $ |\Sigma|^{f(n)}f(n)|Q|\stackrel{rozepíšeme~pomocí~log}{=}2^{f(n)\log_2|\Sigma|}2^{\log_2f(n)}2^{\log_2|Q|}= 2^{f(n)\log_2|\Sigma|+\log_2f(n)+\log_2|Q|}\leq 2^{f(n)\cdot(\log_2|\Sigma|+1+\log_2|Q|)} $. Stačí tedy zvolit $ c_M = (log_2|Σ| + log_2|Q| + 1) $.
- (💡 ani nemusíme používat 2ku stačí nějaká konstanta $ c $)
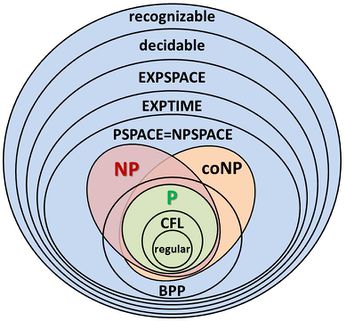
Věta ( Savičova, pro polynomy ): $ NPSPACE = PSPACE $
- Dk (NPSPACE ⊇ PSPACE)
- ∀ DTS je zvláštním případem NTS
- Dk (NPSPACE ⊆ PSPACE - neformální dk, zde zkrácený přepis dk ze skript nebo originální dk ve skriptech)
- Pro NTS (pracující v NPSPACE) zkonstruujeme DTS pracující v polynomiálním prostoru (💡 i když čas může být exponenciální).
- Nechť NTS $ M $ přijímající $ L(M) $ v prostoru $ O(p(n)) $, pak DTS $ M’ $ přijímající stejný $ L $ pracující v polynomiálním prostoru může být zkonstruován pomocí bool rekurzivní funkce $ Dosažitelná(i, K_1, K_2) $, kde K jsou konfigurace NTS $ M $ a i je číslo.
- $ Dosažitelná(i, K_1, K_2) $ vrátí:
- true, pokud je $ K_2 $ dosažitelná z $ K_1 $ v nejvýše i krocích,
- jinak false.
- Tedy volání např $ Dosažitelná(i, K_1, K_2) $ rekurzivně zavolá $ ∀ K $: $ Dosažitelná(⌊i/2⌋, K_1, K) $ a $ Dosažitelná(⌈i/2⌉, K, K_3) $
- (💡 alg. je zřejmě korektní)
- Nechť $ w $ je vstupní slovo, zavoláme $ Dosažitelná(i, K_0, K_F) $ (💡 z počáteční konfigurace do BÚNO jediné přijímající) a $ i = 2^{c_M p(n)} $.
- Potřebujeme $ hloubka=|log( 2 ^ {c_M p(n)} )| = O(p(n)) $ rekurzivních volání a $ prostor(K_i) = O(p(n)) $ místa na každé úrovni rekurze (💡 recyklace, 2 rekurzivní volání mohou používat stejný prostor).
- Tedy $ prostor = hloubka\cdot prostor(K_i) = O(p(n))\cdot O(p(n)) = O(p(n)^2) $ místa na pásce pro všechna rekurzivní volání $ Dosažitelná $.
- Druhá mocnina polynomu je stále polynom a takže: $ NPSPACE = PSPACE $.
| další zdroje |
|---|
|
Věta ( Savičova, obecné znění ): Nechť $ f : N → N $ je funkce vyčíslitelná v prostoru $ O(f(n)) $, pro kterou platí, že $ f(n) ≥ log_2 n $ pro všechna $ n ∈ N $. Potom platí, že $ NSPACE(f(n)) ⊆ DSPACE(f^2(n)) $.
- Dk
- Důkaz předchozí věty nikde nevyužíval žádných zvláštních vlastností polynomů, můžeme jej tedy zobecnit a dostat tak obecnou Savičovu větu.
- Ukázali jsme vlastně, že k otestování toho, jestli v obecném orientovaném grafu $ G=(V, E) $ vede cesta z daného vrcholu $ 0 $ do vrcholu $ F $, stačí prostor $ O((\log_2|V|)^2) $, pokud do tohoto prostoru nepočítáme prostor nutný k uložení grafu.
- Pokud tedy místo polynomu $ p(n) $ použijeme obecnou funkci $ f(n) $, dostaneme tvrzení, že $ NSPACE(f(n))\subseteq DSPACE(f(n)^2) $.