Protiseminár - Otázniky
Otázky & odpovede
- Ako použiť Lagrangián a Hamiltonián v kovariantnom popise častice v poli? Nekovariantne to nie je problém. Pohyb častice medzi pevnými časmi t_1, t_2 minimalizuje účinok
$ S_{12} = \int_{t_1}^{t_2} L dt, $ kde obyčajný Lagrangián je $ L = -mc^2\sqrt{1-\frac{\mathbf v^2}{c^2}} - q\phi + q\mathbf A \cdot \mathbf v. $ Prechod k Hamiltonovskému popisu je jednoduchý - Hamiltonián je $ H = \mathbf p \cdot \mathbf v - L = \sqrt{(\mathbf p - q\mathbf A)^2 c^2 + m^2c^4} + q\phi $ a správne pohybové rovnice sú kde $ \frac{d\mathbf r}{dt} = \frac{\partial H}{\partial \mathbf p}~~~,~~~\frac{d\mathbf p}{dt} = - \frac{\partial H}{\partial \mathbf r}. $
Lenže ak túto procedúru skúsime zopakovať kovariantne, narazíme na problém. Ako vôbec sformulovať princíp účinku kovariantne? Ak budeme integrovať cez vlastný čas, účinok je $ S_{12} = \int_{\tau_1}^{\tau_2} -mc\sqrt{-u_\mu u^\mu} + qA_\mu u^\mu d\tau. $ Ak teraz zmeníme pôvodný princíp účinku na predpoklad, že pri fixovaných hraniciach tau je variácia tohoto integrálu nulová, dostaneme hybnosť $ p_\mu = \frac{mc\frac{dx_\mu}{d\tau}}{\sqrt{-u_\mu u^\mu}} + qA_\mu $ a pohybové rovnice $ \frac{d}{d\tau} \left( \frac{mc\frac{dx_\mu}{d\tau}}{\sqrt{-u_\nu u^\nu}} \right) = q ( \partial_\mu A_\nu - \partial_\nu A_\mu ) u^\nu. $
Lenže pohybové rovnice sú zle, pretože správne rovnice sú bez tej odmocniny a c: $ \frac{d}{d\tau} \left( m\frac{dx_\mu}{d\tau} \right) = q ( \partial_\mu A_\nu - \partial_\nu A_\mu ) u^\nu. $
V knižkách sa tento problém odlfákne tým, že sa po odvodení rovníc povie $ u_\mu u^\mu = -c^2 $. Lenže to je opravovanie rovnice a zakrývanie faktu, že Lagrangián a princíp účinku nám nedali správne rovnice. Väzba $ u_\mu u^\mu = -c^2 $ by mala plynúť z Lagrangiánu. Ďalšou námietkou je, že ak by sme väzbu zobrali skôr, už v Lagrangiáne, dostali by sme $ L = -mc^2 + qA_\mu u^\mu $ z ktorého by sme dostali hybnosť $ p_\mu = qA_\mu $ a rovnice $ (\partial_\mu A_\nu - \partial_\nu A_\mu) u^\nu = 0, $ ktoré sú zle.
Hamiltonovská formulácia nie je na tom vôbec lepšie: keďže Lagrangián je homogénny prvého rádu v rýchlostiach, podľa Eulerovej vety platí $ L = p_\mu u^\mu $ a Hamiltonián $ H = p_\mu u^\mu - L $ je nulový (tzn. nezávisí na hybnostiach a polohách), čo dá úplne nesprávne rovnice $ \mathbf r = const., \mathbf p = const. $
Hlavný problém vzniká, keď sa snažíme použiť vlastný čas - vtedy sa nám do problému dostáva spomenutá väzba. Ak ostaneme pri starom dobrom súradnicovom čase, žiadnu väzbu nemáme - dostaneme rovno rovnice $ \frac{d}{d\tau} \left( \frac{m\mathbf v}{\sqrt{1-\frac{v^2}{c^2}}}\right) = q(\mathbf E + \mathbf v \times \mathbf B). $ Ako to teda správne chápať? Z celej tejto bolestivej procedúry mám pocit, že myšlienka kovariantného zápisu nie je príliš užitočná.
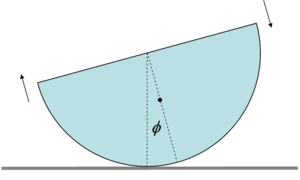
- Predstavme si polguľu na drsnej rovine, takže nedochádza k prešmykovaniu. Polguľa sa môže iba odvaľovať a kmitať. Ako správne napísať pohybovú rovnicu? Z Lagrangiánu
$ L = \frac{1}{2} I_\phi (\dot \phi)^2 + mgr_T \cos \phi $
dostaneme pohybovú rovnicu
$ \frac{d}{dt} \left( I_\phi \dot \phi \right) = \frac{1}{2}I_\phi^\prime\dot{\phi}^2-mgr_T \sin\phi $,
zatiaľčo z druhej impulzovej vety (časová zmena momentu hybnosti = moment sily) máme
$ \frac{d}{dt} \left( I_\phi \dot \phi \right) = -mgr_T \sin\phi $.
Ktorý prístup je správne a ako sa má správne urobiť ten druhý?
- V skutočnosti je správne rovnica z Lagrangiánu. Postup cez moment sily je tiež dobrý, ale zrada je v momente hybnosti: jeho zmenu treba počítať vzhľadom na pevný bod podložky; po infinitezimálnom posunutí dotykového bodu z bodu 1 do bodu 2 na podložke o $ \mathbf a $ je už moment hybnosti zvýšený o príspevok pohybu ťažiska: $ \mathbf L _2 = I_\phi \mathbf \omega + \mathbf a \times m\mathbf{v_T} $, čo po vyjadrení z geometrie dá rovnakú pohybovú rovnicu ako Lagrangián.
- V klasickej mechanike pre účinok S častice, ktorý chápeme ako funkciu jej aktuálnej polohy a času - $ dS(q,t) = L dt = p dq - H dt $ - platia rovnice $ \frac{\partial S}{\partial x^i} = p_i $, $ \frac{\partial S}{\partial t} = -E $. Ako je možné, že je táto rovnica správne kovariantne (dá sa zapísať ako $ \partial_\mu S = p_\mu $) už v klasickej mechanike, kde by sa metrika $ -+++ $ nemala nikde objaviť (to je až výsledok relativity)?
.
- Predstavme si pravidelný mnohosten, napríklad kocku. Každý taký mnohosten má nejaký počet stien 'F', hrán 'E' a vrcholov 'V', pričom tieto tri čísla vždy spĺňajú vzťah $ F + V - E = 2 $. Je ešte jedna oblasť, kde sa objavuje podobný vzťah - termodynamika.
 Gibbsovo pravidlo fáz tvrdí, že pre počet fáz f, zložiek z a počet stupňov voľnosti sústavy s platí vzťah $ f + z - s = 2 $. Existuje tu nejaký súvis, alebo je to všetko iba náhoda ?
Gibbsovo pravidlo fáz tvrdí, že pre počet fáz f, zložiek z a počet stupňov voľnosti sústavy s platí vzťah $ f + z - s = 2 $. Existuje tu nejaký súvis, alebo je to všetko iba náhoda ?
- Myslím, že to je jen náhoda. Výraz $ V+F-E $ se nazývá Eulerova charakteristika a závisí na topologii tělesa, takže může mít i jinou hodnotu než 2.