TIN065 Prednáška 04
| Prednášky z Vyčísliteľnosti II |
| Obsah |
|---|
|
Tak trochu opakovania. ČRFály vieme očíslovať (máme numeráciu) a náš $ \Phi_e $ je rovný $ W_{\rho(e)} $, kde $ \rho $ je regularizačná funkcia. Taktiež vieme, že keď máme funkcionál, tak ak mu predložíme množinu ako orákulum, dostaneme funkciu. A ak tejto funkcii dáme číslo, tak možno dostaneme číslo (podľa toho, či je tá funkcia v tomto čísle definovaná). A tiež vieme, že nám platí s-m-n veta, a to dokonca „stejneměrně“. Teda existuje $ \overline{s_m} $ také, že pre každé A a každé $ \vec{x} $ a každé $ \vec{y} $ niečo (...) platí.
Tiež sme minule definovali operáciu skoku, a to takto: $ A' = \{x: \Phi_x(A)(x)\downarrow\} = \{x: x \in W_x^A\} $ a jej prirodzené iterácie $ A^{(n)} $ pre $ n \in N_0 $ (a keď sa posnažíme, tak dôjdeme až k $ A^{(\omega_0)} $, prípadne aj ďalej).
No, a skončili sme vetou.
Vlastnosti skoku[editovat | editovat zdroj]
- A' je A-rekurzívne spočítateľná
- A' nie je A-rekurzívna
- B je A-rekurzívne spočítateľná práve vtedy, ak B je 1-prevoditeľná na A'
- Ak A je rekurzívne spočítateľná vzhľadom k B a zároveň B je turingovsky prevoditeľná na C $ (B \leq_T C) $, potom A je rekurzívne spočítateľná vzhľadom k C
- $ A \leq_T B \iff A' \leq_1 B' $
- $ A \equiv_T B \iff A' \equiv_1 B' $
Túto vetu sa teraz pokúsime dokázať.
Prvá časť je jednoduchá - A' je A rekurzívne spočítateľná priamo z definície A'. Je vhodné si tiež všimnúť, že toto tvrdenie je obdobné podobnému z Vyčísliteľnosti I: K je rekurzívne spočítateľná množina.
Druhá časť je opäť podobná nerelativizovanému tvrdeniu o K, ktoré hovorí, že K nie je rekurzívna. Dokáže sa to skoro rovnakým spôsobom. Z relativizovanej Postovej vety vieme, že nám stačí dokázať, že doplnok A', teda $ (\overline{A'}) $ nie je A-rekurzívne spočítateľná množina. A to urobíme sporom.
Predpokladajme, že $ \overline{A'} $ je A-rekurzívne spočítateľná. V tom prípade je to jedna z množín $ W^A $ a má svoj index $ x_0: \overline{A'} = W_{x_0}^A $. Z toho jednoducho vyplýva, že $ x_{0} \in \overline{A'} \iff x_{0} \in W_{x_0}^A $. Ďalej z definície skoku množiny A vyplýva, že $ x_0 \in A' \iff x_0 \in W_{x_0}^A $. Zložením týchto dvoch ekvivalencií dostávame spor: $ x_{0} \in \overline{A'} \iff x_{0} \in A' $. Teda $ \overline{A'} $ nemôže byť A-rekurzívne spočítateľná, a teda A' nie je A-rekurzívna.
Tretia časť je tiež podobná Vyčísliteľnosti I, kde sme si povedali, že ak je množina rekurzívne spočítateľná, vieme ju 1-previesť na K.
Dokážme to najprv jedným smerom. Nech $ B \leq_1 A' $. To znamená, že máme prostú ORF $ f $ takú, že $ x \in B \iff f(x) \in A' \iff f(x) \in W_{f(x)}^A \iff \Phi_{f(x)}(A)(f(x))\downarrow $ (postupne definícia 1-prevoditeľnosti, definícia A' a nakoniec definícia $ W_{f(x)}^A $. A to posledné už je A-rekurzívne spočítateľná podmienka.
A teraz opačný smer. Nech B je A-rekurzívne spočítateľná množina. Použijeme rovnaký dôkaz ako vo Vyčísliteľnosti I (podľa skrípt Petra Hoška). Nech $ y \in B = W_{x_1}^A $. Vytvoríme si funkciu $ \alpha^A $ takto: $ \alpha^A(x1, y, w)\downarrow \iff \Phi_{x_1}(A)(y)\downarrow \iff y \in B $ (prvá ekvivalencia je definícia funkcie $ \alpha^A $ a druhá je definícia množiny $ B $, keďže $ B = W_{x_1}^A $). Nech funkcia $ \alpha^A $ má index $ a $, teda nech $ \alpha^A \simeq \Phi_a(A)(x_1, y, w) \simeq \Phi_{\overline{s_2}(a, x_1, y)}(A)(w) $. Položme $ w = \overline{s_2}(a, x_1, y) $. Potom $ y \in B $$ \iff $$ y \in W_{x_1}^A $$ \iff $$ \alpha^A(x_1, y, w)\downarrow $$ \iff $$ \Phi_{\overline{s_2}(a, x_1, y)}(A)(\overline{s_2}(a, x_1, y))\downarrow $$ \iff $$ \overline{s_2}(a, x_1, y) \in A' $. Potom $ \overline{s_2}(a, x_1, y) $ je dokonca prostá PRF, nie iba ORF, ktorá 1-prevádza B na A'.
Štvrtú časť dokážeme "intuitívne". Nech A je B-rekurzívne spočítateľná a B je rekurzívna v C. To znamená, že máme program $ P_1 $, ktorý pomocou B vie efektívne generovať A a program $ P_2 $, ktorý pomocou C dokáže rozhodovať B. A tvrdíme, že existuje program $ P_3 $, ktorý pomocou C efektívne generuje A. Tento program $ P_3 $ vytvoríme jednoducho. Vezmeme program $ P_1 $, ktorý efektívne generuje A a tam, kde sa pokúsi spýtať sa na B, vložíme podprogram $ P_2 $, ktorý stále zastaví a bude sa pýtať už iba na C.
Všimnite si, že veta, v ktorej sa predpoklady obrátia už neplatí: Teda nie je pravda, že ak A je B-rekurzívna a B je C-rekurzívne spočítateľná, potom A je C-rekurzívne spočítateľná. Prečo? Ako protipríklad môžeme uviesť napríklad množinu $ \overline{K} $, pre ktorú určite platí, že je rekurzívna vzhľadom ku K ($ \overline{K} \leq_T K $). Taktiež pre K určite platí, že je rekurzívne spočítateľná vzhľadom k $ \emptyset $, teda rekurzívne spočítateľná (bez orákula). Ale už vôbec neplatí, že $ \overline{K} $ je rekurzívne spočítateľná, čo by z takejto vety s obrátenými predpokladmi vyplývalo.
Tu sa hodí malé pripomenutie: A-rekurzívne spočítateľná množina je buď definičný obor nejakej A-ČRF alebo (a to sa nám často hodí viac) obor hodnôt nejakej A-ČRF. Obe tieto charakteristiky sú ekvivalentné.
A ešte triviálny dôsledok tretej časti, ktorý sa nám bude hodiť v dôkaze piatej časti: A je 1-prevoditeľná na $ A' $. Platí to preto, lebo A je A-rekurzívna, takže je aj A-rekurzívne spočítateľná, a preto sa dá 1-previesť na A'.
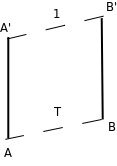
Piata a šiesta časť je dôležitá a na lepšie pochopenie sa nám hodí obrázok:
Vždy poznáme vzťah (zhora dole) medzi A a $ A' $ a medzi B a $ B' $. A tvrdenie nám hovorí, že ak máme jeden zo vzťahov medzi A a B alebo medzi $ A' $ a $ B' $, tak ten druhý vieme.
Idea je taká, že ak potrebujeme vedieť vzťah medzi A a B, tak pôjdeme cestou zhora: $ A \rightarrow A' \rightarrow B' \rightarrow B $. Na druhej strane, ak potrebujeme vedieť vzťah medzi $ A' $ a $ B' $, tak pôjdeme cestou zdola.
Tvrdenie:$ A \leq_T B \iff A' \leq_1 B' $
Dôkaz:
- $ \Longrightarrow $: $ A \leq_T B $ a A' je A-rekurzívne spočítateľná. Z toho podľa štvrtej časti dostaneme, že A' je B-rekurzívne spočítateľná. A podľa tretej časti z tohto ďalej zistíme, že $ A' $ je 1-prevoditeľná na $ B' $.
- $ \Longleftarrow $: $ A' \leq_1 B' $. $ A $ aj $ \overline{A} $ sú obe zrejme A-rekurzívne a teda sú aj A-rekurzívne spočítateľné, preto sú obe 1-prevediteľné na $ A' $. Keďže 1-prevoditeľnosť je tranzitívna, tak sú aj 1-prevoditeľné na $ B' $, čo ale znamená, že sú obe B-rekurzívne spočítateľné, a teda z relativizovanej Postovej vety vyplýva, že A je B-rekurzívna (čo je len iný názov pre $ A \leq_T B $).
Šiesta časť tvrdenia je triviálnym dôsledkom piatej.
Skok na T-stupňoch[editovat | editovat zdroj]
Body 5 a 6 predchádzajúceho tvrdenia nám umožňujú zaviesť skok aj na T-stupňoch. Pre pripomenutie, T-stupeň je jedna trieda ekvivalencie $ \equiv_T $. Ak máme A a B, ktoré sú na seba T-prevoditeľné (sú v jednom T-stupni), tak ich skoky A' aj B' sú tiež v jednom T-stupni. Ale 6. bod predchádzajúcej vety dokonca hovorí, že ich skoky nielen, že sú v jednom T-stupni, ale sú dokonca v jednom 1-stupni (teda $ A' \equiv_1 B' $).
A teda skok $ [a]' $ definovaný ako $ deg_T(A') = \{B:B\equiv_T A'\} $ pre ľubovoľné $ A \in [a] $ je korektne definovaný. Môžeme si takto zaviesť aj skoky o viac ako jeden stupeň: ($ [a]'', [a]^{(3)}, \dots $) a to tak, že $ [a]^0 = [A] $ a $ [a]^{(n+1)} = ([a]^{(n)})' $.
Poznámka: Vďaka uniformnosti by sa dalo definovať aj niečo ako $ [a]^\omega $.
Trošku o uniformnosti[editovat | editovat zdroj]
Veta o základných vlastnostiach operácie skoku platí uniformne. To, že A' je A-rekurzívne spočítateľná platí pre všetky A. Presnejšie: $ (\exists z_0)(\forall A)(A' = W_{z_0}^A) $ alebo tiež $ (\exists z_1)(\forall A)(\Phi_{z_1}(A) \mathrm{\ generuje\ } A') $.
Dôkaz: Vezmime si rekurzívne spočítateľnú množinu $ \{<\sigma, x, y>: <\sigma, x, y>\in W_{\rho(x)}\} $ a označme si ju $ W_{z_0} $. Je vhodné si všimnúť, že $ W_{z_0} $ je regulárna, teda $ W_{z_0} = W_{\rho(z_0)} $.
$ x \in A' \iff \Phi_x(A)(x)\downarrow \iff (\exists \sigma)(\exists y)(<\sigma, x, y> \in W_{\rho(x)} $ & $ \sigma \leq A) $$ \iff $$ (\exists \sigma)(\exists y)(<\sigma, x, y> \in W_{z_0} $ & $ \sigma \leq A) $$ \iff $$ x \in W_{z_0}^A $
Podobná uniformosť platí aj pre $ A\leq_T B \iff A' \leq_1 B' $. Aj tam existuje ORF $ f $ taká, že ak pre A a B platí, že $ A \leq_T B $ pomocou funkcie s indexom $ z $ (teda $ \Phi_z(B) = C_A $), tak potom $ A' \leq_1 B' $ pomocou funkcie s indexom $ f(z) $.
Limitná vyčísliteľnosť[editovat | editovat zdroj]
Touto sa bude zaoberať ďalšia prednáška, takže len zhruba.
Vezmime si množinu $ A $, ktorá je rekurzívne spočítateľná. To znamená, že je definičným oborom nejakej ČRF $ f $. Vytvoríme si funkciu $ g(x, y) $ takú, že $ (\forall x)(g(x, 0) = 0) $ a $ g(x, y) $ bude $ 1 $ práve vtedy, ak za $ y $ krokov $ x $ padlo do $ A $, teda ak za $ y $ krokov ČRF $ f $ zastaví. V opačnom prípade položíme $ g(x, y) = 0 $.
Nakreslíme si „graf funkcie $ g $“. Na vodorovnú os dáme $ x $ a na zvislú tradične $ y $ a všimneme si stĺpce nad jednotlivými $ x $ (všetko sú stále funkcie nad prirodzenými číslami). Stĺpce, kde $ x $ nie je prvkom $ A $ sú celé nulové (po žiadnom počte krokov nepadne $ x $ do $ A $). Stĺpce, kde $ x $ je prvkom $ A $, sú spočiatku nulové, ale časom sa zmenia na jednotku a ďalej sa nemenia (keď po $ y $ krokoch $ x $ padne do $ A $, tak už z neho nevypadne).
V každom stĺpci je maximálne jedna zmena z nuly na jednotku (a nikdy nie späť). Tomu hovoríme 1-rekurzívne spočítateľné množiny.
Potom máme 2-rekurzívne spočítateľné množiny. Tie majú v každom stĺpci maximálne dve zmeny. Takéto množiny odpovedajú rozdielu dvoch rekurzívne spočítateľných množín $ A \setminus B $ (Najprv zistíme, že $ x \in A $, ale potom neskôr môžeme zistiť, že $ x \in B $ a tým pádom sa hodnota znova zmení na nulu).
Nie je ťažké predstaviť si, ako tento postup môžeme rozšíriť a zadefinovať si n-rekurzívne spočítateľné množiny pre všetky $ n \in N $ - jednoducho tam bude najviac $ n $ zmien (ktoré odpovedajú boolovskej kombinácií nanajvýš $ n $ rekurzívne spočítateľných množín).
Tiež sa dá definovať $ \omega_0 $ rekurzívne spočítateľná množina. V tom prípade budeme mať nejakú ORF $ g $ takú, že v stĺpci $ j $ bude najviac $ g(j) $ zmien. Máme teda odhad počtu zmien v každom stĺpci, ale globálny odhad pre všetky stĺpce nemusí existovať.
A potom si ešte zadefinujeme limitnú vyčísliteľnosť. $ A $ je limitne vyčísliteľná práve vtedy, ak existuje ORF $ h $ (s oborom hodnôt $ \{0, 1\} $) taká, že $ (\forall x)(A(x) = \lim_{s \to \infty} h(x, s)) $. Tá limita znamená, že pre dostatočne veľké $ s $ sa už hodnota funkcie $ h $ nemení, čiže v každom stĺpci bude síce konečne veľa zmien, ale nemusí existovať efektívny horný odhad toho, aký veľký tento počet bude, a to ani globálny, ale ani pre jednotlivé stĺpce.